8. Als laatste voorwaarde is nog gegeven dat
8. Als laatste voorwaarde is nog gegeven dat x-2
 y
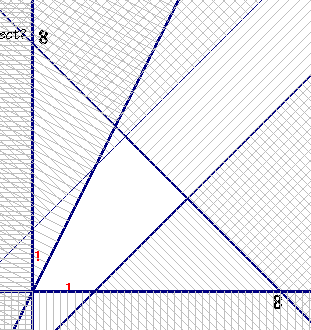
y x+2. Gevraagd wordt het domein van f te te tekenen. Ik ben van het volgende uit gegaan
x+2. Gevraagd wordt het domein van f te te tekenen. Ik ben van het volgende uit gegaan x-2=y
y=x+2
x+y=8
Wanneer ik deze lijnen zou tekenen krijg ik geen gesloten domein. Eerlijk gezegd weet ik niet wat te doen en tast wat in het donker wat nu te doen, kunt u mij helpen wat de bedoeling is?
M.d.v.G
wouter
14-2-2003