WisFaq!

Inductieve en deductieve bewijzen

Wat is het verschil in de wiskunde tussen "inductieve bewijzen" en "deductieve bewijzen"? Indien mogelijk, graag een eenvoudig voorbeeld als illustratie.

D. Angela
26-4-2015

Antwoord

Deze vraag leidde bij ons tot een aardige discussie. Uiteindelijk leverde dit het volgende op:

Deductief bewijs: dit lijkt vrij duidelijk. Vanuit algemene uitspraken (ik neem hier even aan dat deze juist zijn) wordt via logisch redeneren aangetoond dat een nieuwe bewering juist is. Een voorbeeld is:

We weten dat voor alle driehoeken geldt dat de som van de hoeken 180° is (dit is de algemene uitspraak).
Nu nemen we een driehoek ABC, waarin hoek A=60° en hoek B=40°. Dan kunnen we berekenen:
Hoek C = 180-60-40 = 80°

Omdat alle driehoeken deze eigenschap hebben, en ABC een driehoek is, moet ABC ook wel deze eigenschappen hebben. Via deze weg kunnen we bewijzen dat hoek C 80° is.

Inductie komt erop neer dat een (algemeen geldende) conclusie wordt getrokken uit ondersteunende argumenten. Een bekend voorbeeld is: "de eerste zwaan die ik zie, is wit. De tweede zwaan is wit, de derde zwaan is wit enz. Conclusie: alle zwanen zijn wit". Deze conclusie is misschien wel aannemelijk, maar hoeft niet juist te zijn: het is mogelijk dat ergens toch een zwarte zwaan verstopt zit.
Een ander voorbeeld is de conclusie dat leven afhankelijk is van vloeibaar water. We kennen zeer vele levensvormen, al deze levensvormen zijn afhankelijk van vloeibaar water. Ook al kunnen we ons geen leven zonder vloeibaar water voorstellen, het kan niet worden uitgesloten dat ook leven zonder vloeibaar water mogelijk is.

Wiskundig gezien is zo'n conclusie geen bewijs, in de wiskunde bestaat dus geen inductief bewijs. We spreken dan liever van een vermoeden. Een bekend voorbeeld is het vermoeden van Goldbach. Dit vermoeden luidt:

"Elk even getal groter dan 2 kan geschreven worden als de som van twee priemgetallen."

Met behulp van computers is al gecontroleerd dat dit vermoeden klopt voor getallen tot 4x10¹⁸. Inductief kunnen we beredeneren dat zoveel aanwijzingen het wel heel erg waarschijnlijk maken dat dit vermoeden klopt voor alle getallen, maar bewezen is het niet ...

Verwarrend (en dus bron voor onze discussie) is het principe van 'volledige inductie'. Met deze techniek kan je een uitspraak bewijzen voor een oneindige rij getallen, op deze manier:

• Laat zien dat de uitspraak klopt voor het eerste getal, en:
  
• Laat zien dat, als de uitspraak klopt voor een willekeurig getal, de uitspraak ook klopt voor het volgende getal.

Omdat de uitspraak klopt voor getal nummer 1, klopt deze dus ook voor getal nummer 2, en daarmee ook voor getal nummer 3, enz, dus voor alle getallen.

Een voorbeeld is:

Bewijs dat de som van n getallen 2, 4, 6 enz gelijk is aan n(n+1). In formule:



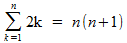
Gemakkelijk is te zien dat dit klopt voor n=1: de som van alleen het eerste getal is 2 en inderdaad geldt:

2 = 1(1+1)

Nu nemen we aan dat de uitspraak waar is voor een bepaalde waarde van n. We nemen dan het volgende getal m=n+1 en gaan bekijken of de uitspraak dan ook waar is voor dit nieuwe getal m. Onze 'nieuwe' rij bestaat uit de oorspronkelijke rij met als extra getal 2m=2(n+1):



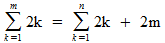
Het eerste deel kenden we al, het tweede deel kunnen we anders schrijven:



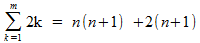
Twee termen samenvoegen:



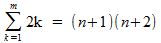
Zodat we uiteindelijk krijgen:



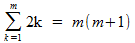
Onze conclusie is dus: wanneer de uitspraak waar is voor n, dan is deze ook waar voor n+1.

We wisten al: de uitspraak is waar voor n=1, dus ook voor n=2
de uitspraak is waar voor n=2, dus ook voor n=3
de uitspraak is waar voor n=3, dus ook voor n=4
enz.

Verwarrend is dat deze techniek van bewijzen (volledige inductie) niet gerekend wordt tot inductief redeneren ....

Zie Wikipedia: deductive reasoning [https://en.wikipedia.org/wiki/Deductive_reasoning]

GHvD
28-4-2015