WisFaq!

Bezierkromme

Ik heb een kwadratische bezierkromme met de volgende punten: P₀=(0,0) en P₂=(1,0). Ook is de top van de kromme gegeven (deze kan variëren maar we nemen (0.25,0.75) als voorbeeld). Ik wil een formule opstellen om de positie van P₁ te kunnen berekenen, is dit mogelijk?
Alvast bedankt

Jarvis
13-4-2015

Antwoord

Volgens Wikipedia | Kwadratische Bezierkromme moet gelden:

$
B(t) = \left( {1 - t} \right)^2 P_0 + 2t\left( {1 - t} \right)P_1 + t^2 \cdot P_2 \,\,voor\,\,t \in [0,1]
$

Met P₀=(0,0), P₁=(x,y) en P₂=(1,0) geldt:

$
\begin{array}{l}
B(t) = \left\{ \begin{array}{l}
2t\left( {1 - t} \right)P_1 + t^2 \\
2t\left( {1 - t} \right)P_1 \\
\end{array} \right. \\
B(t) = \left\{ \begin{array}{l}
2t\left( {1 - t} \right) \cdot x + t^2 \\
2t\left( {1 - t} \right) \cdot y \\
\end{array} \right. \\
\end{array}
$

Oftewel:

$
\left\{ \begin{array}{l}
x = \frac{{4t^2 - 1}}{{8t(t - 1)}} \\
y = \frac{3}{{8t(1 - t)}} \\
\end{array} \right.
$

Voor de 'top' van de kromme geldt:

$
y' = 0 \Rightarrow t = \frac{1}{2}
$

Invullen geeft:

$
\begin{array}{l}
\left\{ \begin{array}{l}
x = \frac{{4\left( {\frac{1}{2}} \right)^2 - 1}}{{8 \cdot \frac{1}{2}(\frac{1}{2} - 1)}} = 0 \\
y = \frac{3}{{8 \cdot \frac{1}{2}(1 - \frac{1}{2})}} = 1\frac{1}{2} \\
\end{array} \right. \\
B(t) = \left\{ \begin{array}{l}
t^2 \\
2t\left( {1 - t} \right) \cdot 1\frac{1}{2} \\
\end{array} \right. \\
B(t) = \left\{ \begin{array}{l}
t^2 \\
3t\left( {1 - t} \right) \\
\end{array} \right. \\
\end{array}
$

...en dan ben je er wel. Het punt $P_1$ heeft als coördinaten $(0,1\frac{1}{2})$.



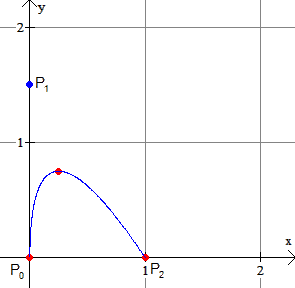
Zoiets moet het zijn. Zou het daarmee lukken?

WvR
13-4-2015