WisFaq!

Zwaartepunt van omwentelingslichaam

Hoi, ik heb een vraag over het zwaartepunt van een omwentelingslichaam berekenen.

Ik heb de formule f(x) = e^2x en die wordt ingesloten door x = 1, x = 2 en de x-as. De vraag is om het zwaartepunt te berekenen bij rotatie om de y-as.

Hoe moet ik dit aanpakken? Ik kan het nergens in mijn boeken en op internet vinden (mijn leraar heeft de vraag zelf gemaakt namelijk).

Dianne
7-4-2015

Antwoord

Hallo Dianne,

Ik hoop dat je voldoende papier hebt en deelberekeningen overzichtelijk noteert, want het wordt een hele berekening !

In de figuur zie je een schets van de functie, het groene vlak wordt gewenteld rond de y-as.



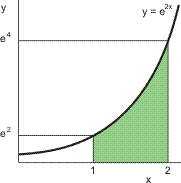
Vanwege symmetrie ligt het zwaartepunt op de y-as, dus de x-coördinaat van het zwaartepunt is nul. We hoeven dus alleen de y-coördinaat van het zwaartepunt te berekenen.

Waarschijnlijk heb je wel formules geleerd over omwentelingslichamen om de horizontale (x-)as. Om hierbij aan te sluiten, verwissel ik de horizontale en de verticale as, zie de linker figuur hieronder.



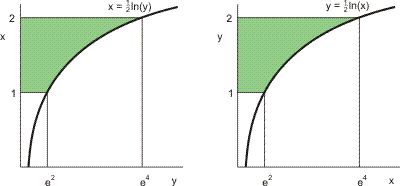
Dan is het ook wel handig om x als functie van y te schrijven in plaats van andersom:

y = e2x
ln(y) = 2x
x = 1/2ln(y)

Tot slot verwissel ik de naam van de variabelen (x wordt y en andersom). Dit is niet echt nodig, maar zo zijn we het gewend, dat scheelt weer vergissingen.

Nu is de vraag: bereken de x-coördinaat van het zwaartepunt van het omwentelingslichaam dat ontstaat bij omwenteling rond de x-as.

Om dit op te lossen, bekijk ik de 4 vlakdelen I, II, III en IV, zie deze figuur:



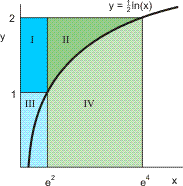
Het omwentelingslichaam ontstaat door eerst alle vlakdelen te wentelen om de x-as, en daar weer van af te trekken de omwentelingslichamen van de vlakdelen III en IV. Van alle omwentelingslichamen heb ik nodig:

• de inhoud
  
• de plaats van het zwaartepunt

Eerst maar eens de vlakdelen I en III wentelen. Dit levert een cilinder met straal 2 en hoogte e². De inhoud van een cilinder berekenen we met pr²h, dus:

Inhoud_I+III = p2².e² = 4pe²

Op gelijke wijze vind ik:

Inhoud_III= pe², dus:

• Inhoud_I = 3pe²
  
• Inhoud_III = pe²

De zwaartepunten van I en III liggen op de halve hoogte, dus:

• x_zI=¹/₂e²
  
• x_zIII=¹/₂e²

Ook de inhoud van II+IV en het zwaartepunt vinden we met de formule voor een cilinder:

• Inhoud_II+IV = 4p(e⁴-e²)
  
• x_{z II+IV} = ¹/₂(e⁴+e²)

Dan de inhoud van IV. Hiervoor moeten we een integraal opstellen:

Inhoud_IV = òpy²·dx

Dus:

Inhoud_IV = ò(¹/₂ln(x))².dx, x van e² tot e⁴

Het is even rekenen, maar je vindt:

• Inhoud_IV = ¹/₂pe²(5e²-1)

Dan het lastigste stuK: het zwaartepunt van IV. Hiervoor geldt de formule:



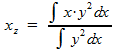
Uitleg over deze formule vind je bij Zwaartepunt van een omwentelingslichaam. Voor jouw situatie moet je dus berekenen:



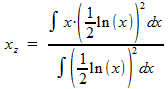
Na vereenvoudigen wordt dit:



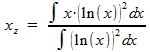
Het is weer even rekenen, maar ik vind uiteindelijk:



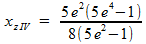
Tot slot nog even de inhoud en het zwaartepunt voor allevier de vlakken samen:

• Inhoud_totaal=p2²e⁴ = 4pe⁴
  
• x_{z totaal}=¹/₂e⁴

Nu hebben we alle 'ingrediënten' verzameld. We moeten de deelvolumes en deelzwaartepunten nog combineren. In het algemeen kan je deelvolumes en deelzwaartepunten op deze manier combineren tot één totaalvolume en totaalzwaartepunt:

I_totaal·x_{z totaal} = I₁·x_z1 + I₂·x_z2 + I₃·x_z3 + ...

Hier geldt dus:

I_totaal·x_{z totaal} = I_I+II·x_{z I+II} + I_III·x_{z III} + I_IV·x_{z IV}

dus ook:

I_I+II·x_{z I+II} = I_totaal·x_{z totaal} - I_III·x_{z III} - I_IV·x_{z IV}

Het gevraagde zwaartepunt van I+II vinden we dan met:



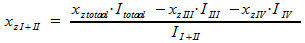
Nu is het zaak om alles netjes in te vullen, dan moet het gevraagde zwaartepunt eruit komen.

Lukt het hiermee?

GHvD
8-4-2015