WisFaq!

Een vaas die 10 ballen bevat

Hello,

Ik moet bij deze echt geholpen worden, ik geraak er echt niet:

Een vaas bevat 10 ballen, genummerd van 1 tot en met 10. Er worden, met teruglegging, zes ballen aselect uit de vaas genomen. Bereken de kans dat:

1) er viermaal een 10 getrokken wordt;
2) er zes verschillende nummers worden getrokken;
3) de zes nummers opeenvolgende natuurlijke getallen zijn;
4) er hoogstens één 10 getrokken wordt.

Bij de 1) denk ik de oplossing te hebben gevonden, maar ik ben niet zeker dat mijn redenering correct is:

# gunstige uitkomsten = (6! . 9²):(4! 2!) = A
# totaal uitkomsten = 10⁶ = B

En dus A/B = 0,1215% - is dit al correct?

Voor de rest weet ik echt nauwelijks hoe beginnen, kan u mij alstublieft helpen?

Dank bij voorbaat,

Dylan
14-3-2015

Antwoord

Hallo Dylan,

Bij opgave 1 begrijp ik niet goed hoe je aan jouw berekening van de teller komt (A), de uitkomst is wel correct. Mijn redenering zou zijn:

- Er moet 4 keer een 10 getrokken worden (kans is steeds 1/10) en 2 keer een ander nummer (kans is steeds 9/10). Het aantal mogelijke volgordes van deze nummers is een combinatie van 4 uit 10 (combinatie van 2 uit 10 mag ook, dit is hetzelfde aantal).

De kans op vier keer nummer 10 is dan:



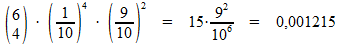
2)
Het eerste numme mag alles zijn. Hiervoor zijn dus 10 mogelijkheden.
Het tweede nummer mag niet gelijk zijn aan het eerste. Hiervoor zijn dus nog 9 mogelijkheden.
Het derde nummer moet ook weer verschillen van de eerste 2: 8 mogelijkheden.
Voor het vierde nummer zijn nog 7 mogelijkheden over.
Het totaal aantal gunstige mogelijkheden is zodoende 10x9x8x7. Deel dit door het totaal aantal mogelijkheden (10⁶) en je hebt de gevraagde kans.

3)
Bepaal het aantal gunstige mogelijkheden door na te gaan op hoeveel manieren je 6 opeenvolgende getallen kunt krijgen. Je kunt bijvoorbeeld wel starten met 1 of 2, maar niet met 8.

4) Hoogstens één 10 betekent: geen enkele 10 of één keer een 10. Bepaal deze kansen afzonderlijk en tel ze op.

Kan je hiermee verder?

GHvD
14-3-2015