WisFaq!

Ontbinden in factoren

Het ontbinden in factoren is me duidelijk wanneer je twee factoren krijgt, ik kan echter nergens wat vinden over het ontbinden in 3 factoren.

Neem bijvoorbeeld dit: x³+7x²-10x-16. Dit zou ontbonden in factoren uit moeten komen op (x+1)(x-2)(x+8). Waarschijnlijk is dit vrij simpel, maar ik denk dat ik iets over het hoofd zie want ik kom hier zelf niet op uit.

Ik kan hier ook geen duidelijke uitleg over vinden in mijn boek of op het internet.

• Ontbinden in factoren

Luc
26-1-2015

Antwoord

Je lost dit op met de factorstelling. Het is gebruikelijk om eerst te kijken of x=1, x=-1, x=2 of x=-2 'toevallig' nulpunten zijn van je veelterm. In dit geval blijkt dat x=-1 en x=2 beide nulpunten te zijn. Het wordt dan zoiets als:

(x+1)(x-2)(...)

In je veelterm staat -16 dus die derde factor zal wel 'x+8' zijn. De veelterm laat zich ontbinden als:

x³+7x²-10x-16=(x+1)(x-2)(x+8)

Voorbeeld
Ontbind x³+4x²-31x-70 in factoren.

Proberen leert dan x=-2 een nulpunt is. Je kunt dan een staartdeling maken met x+2:

$
\eqalign{
& x + 2/x^3 + 4x^2 - 31x - 70\backslash x^2 + 2x - 35 \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,x^3 + 2x^2 \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,2x^2 - 31x - 70 \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,2x^2 + 4x \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - 35x - 70 \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - 35x - 70 \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,0 \cr}
$

...en x²+2x-25 laat zich ontbinden als (x+7)(x-5) dus:

x³+4x²-31x-70 = (x+2)(x-5)(x+7)

Helpt dat?

Naschrift

Zoiets kan ook met de regel van Horner. In het schema geef je in de bovenste regel de coëfficiënten van de veelterm die je wil ontbinden en in het linker vakje het gekende nulpunt.

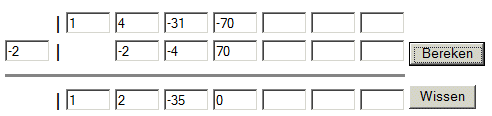
Zie Staartdeling [https://www.google.nl/search?q=staartdeling+veelterm&restrict=Nederlands&btnG=Zoeken&sitesearch=wisfaq.nl]

WvR
26-1-2015