$
\eqalign{\int\limits_{ - \frac{1}
{2}\pi }^{0{,}25268...} {\cos (x) - 2\sin (2x)} \,dx \approx 3{,}125}
$
geeft:
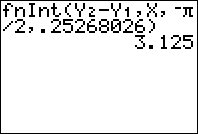
De rest gaat precies zo, maar dan anders...:-)
- Zie ook Oppervlakte van functies
WvR
11-12-2014
Nee dat was geen antwoord op mijn vraag. Om een gebied te berekenen op de TI moet je, zo ver ik weet eerst het gebied onder de bovenste functie berekenen en vervolgens daar het stukje onder de onderste functie tot x van aftrekken.
Mijn vraag: kan dat niet in een keer op de rekenmachine. Gezien je antwoord zal dat wel niet. Als dat wel mogelijk is verneem ik het graag.edward Blaauwgeers
11-12-2014
Nee, dat gaat inderdaad niet zomaar. Je moet de integraal van de 'bovenste functie' min de 'onderste functie' nemen. Zie de link hieronder. Maar in het interval $[-\frac{1}{2}\pi,\pi]$ draait 'boven' en 'onder' steeds om, dus dat is lastig. Maar waarom moeilijk doen? De oppervlakten van de 4 gebieden zijn apart met je GR vrij eenvoudig te bepalen.
$
\eqalign{\int\limits_{ - \frac{1}
{2}\pi }^{0{,}25268...} {\cos (x) - 2\sin (2x)} \,dx \approx 3{,}125}
$
geeft:
De rest gaat precies zo, maar dan anders...:-)
- Zie ook Oppervlakte van functies
WvR
11-12-2014
#74509 - Integreren - Leerling bovenbouw havo-vwo