WisFaq!

Oppervlakte van gebieden

Hallo,

Ik heb moeite met de volgende opgave;

Gegeven: f(x)= 2sin(2x) en g(x)= cos(x) met domein $[-\frac{1}{2}\pi{,}\pi]$.

Bereken in 2 decimalen de totale oppervlakte van de gebieden die worden ingesloten door f en g.

Het totale oppervlak bestaat uit drie gedeelten. Het gedeelte links beslaat [-1/5$\pi$, tot 0.253]. Om dit met mijn TI84 te berekenen heb ik eerst het deel van -1/5pi tot aan 0 gedaan. Vervolgens de functies gespiegeld en het domein 0 tot 0.253 berekend. Daarna het gedeelte onder de x-as. Dit alles om het eerste gebied te berekenen.

Een methode om het gehele eerste linker gebied ineens te berekenen kan ik niet vinden. Is het mogelijk om het gehele gebied, in dit geval het linker ineens te arceren op de TI.

edward Blaauwgeers
10-12-2014

Antwoord

Neem:
Y1=2·sin(x)
Y2=cos(x)
WINDOW:[$-\frac{1}{2}\pi$,$\pi$][-3,3]

Als je de grafieken plot dan krijg je:

®

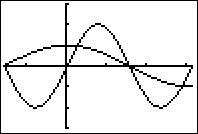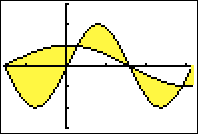
Dat zijn 4 gebieden. Je kunt de snijpunten aflezen:

®

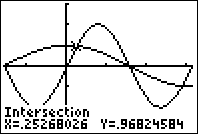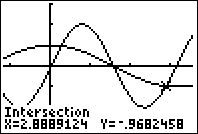
Je krijgt dan zoiets als:

I.
$
\eqalign{\int\limits_{ - \frac{1}
{2}\pi }^{0{,}25268...} {\cos (x) - 2\sin (2x)} \,dx \approx 3{,}125}
$

II.
$
\eqalign{\int\limits_{0,25268...}^{\frac{1}
{2}\pi } {2\sin (2x) - \cos (x)} \,dx \approx 1{,}125}
$

Idemdito voor gebied III. en IV.. Dat geeft (ook) 1,125 voor III. en 0,125 voor IV. Uiteindelijk kom je dan uit op $5\frac{1}{2}$.

Helpt dat?

WvR
11-12-2014