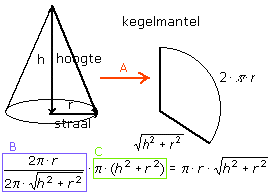
Die B is de omtrek van de grondcirkel van de kegel gedeeld door de omtrek van grote cirkel als je de kegelmantel zou uitvouwen (A). Je weet dan met welk deel van de grote cirkel je te maken hebt als je kijkt naar de cirkelmantel.
Ik heb een uitdrukking (bij C) van de oppervlakte van de grote cirkel. Een B-de deel van C wordt ingenomen door de kegelmantel. Vermenigvuldigen geeft dan een uitdrukking van de oppervlakte van de kegelmantel.
Meer moet het niet zijn...

WvR
13-11-2014