Beste,
Tijdens wiskunde zijn we nu bezig met extremumproblemen. Als taak hebben we er een gekregen en ik zit helemaal vast. Onze opdracht was om een maximum (en de daarbij horende breedte en hoogte) te berekenen van een Romaans venster (dus een halve cirkel op een rechthoek)...
Gegeven is de omtrek: 12 meter.
Om te beginnen had ik voor de opp de formule: l (=lange zijde rechthoek)·x + (p/4·x). Dan heb ik een nevenwaarde voor l gevonden: 6-1,2854x. Dan heb ik l ingevuld maar nu zit ik vast... Kun je mij helpen? Deze taak is erg belangrijk...
Alvast bedankt!!!!Emily
18-10-2014
Hoe pak je dat aan?
Eerst maar 's een tekening en een aantal variabelen kiezen:
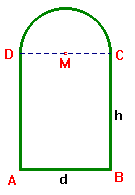
De omtrek is 12. Hiermee kan je $h$ uitdrukken in $d$. Je kunt de oppervlakte ook uitdrukken in $h$ en $d$. Als je daarna $h$ vervangt door de uitdrukking die je gevonden hebt n.a.v. de omtrek krijg je de oppervlakte uitgedrukt in $d$. Je kunt dan met de afgeleide de waarde van $d$ bepalen voor de maximale oppervlakte.
Probeer 't maar 's!
WvR
18-10-2014
#74102 - Differentiëren - 2de graad ASO
