Beschouw het oppervlak in R3 dat gegeven wordt door de grafiek van de functie f : f(x,y) = 1+x2-y2. Welke punten liggen het dichtst bij de oorsprong (0,0,0)? Gebruik de tweede-orde-conditie.
Ik had het volgende gedaan:
D1f(x,y) = 2x, D2f(x,y) = -2y maar wanneer ik deze gelijk stel aan nul krijg ik als kritiek punt (0,0) wanneer ik dan D11f(x,y) bereken is dit 2 en D22 f(x,y) is -2 de discriminant gaat dan negatief zijn waardoor ik met een zadelpunt ga zitten.
De oplossing geeft echter: $(0,\frac{1}{\sqrt{2}},\frac{1}{2})$ en $(0,-\frac{1}{\sqrt{2}},\frac{1}{2})$
Kunnen jullie me hier mee verder helpen? Alvast heel erg bedankt.sophia
11-8-2014
Je moet kijken naar de afstand tot de oorsprong. Je kunt een functie van twee variabelen bedenken waarmee je voor een willekeurig punt de afstand tot O kan berekenen:
$d(x,y)=\sqrt{x^2+y^2+(1+x^2-y^2)^2}$
De vraag is nu: wat is kleinste afstand? In dat geval kan je beter kijken naar deze functie:
$d(x,y)=x^2+y^2+(1+x^2-y^2)^2$
Stationaire punten bepalen... en zo...?
Helpt dat?
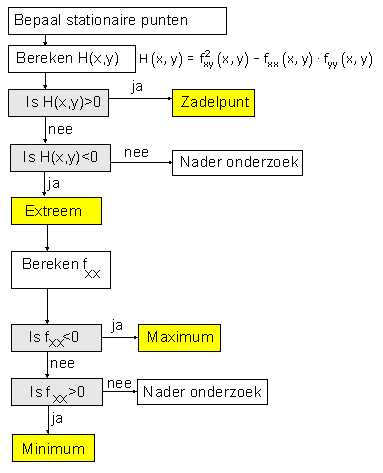
Vragen als 'wat is de kleinste afstand?' nodigen altijd uit tot het formuleren van een functie voor de afstand. In je cursus heb je geleerd hoe je dat minimum kunt vinden.
WvR
11-8-2014
#73663 - Functies en grafieken - Student universiteit België
