WisFaq!

Bewijs continuïteit

Hoe toon je aan dat een functie f niet continu is in een punt a element van A?

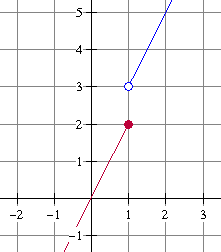
De functie:
x $\to$ 2x als x $\le$1
x $\to$ 2x+1 als x $\gt$ 1

Ik dacht voor xk volgende rij te nemen: ((1/xk)+1) ?
En dan vervolgens te laten convergeren naar a maar ik zit dan vast. Hoe ga ik best te werk?

sophia
28-7-2014

Antwoord

Als $x=1$ dan is $f(x)=2$ maar als je van 'rechts komt' is $f(x)=3$.



Niet continu dus.

WvR
28-7-2014