Je zegt: "Om te weten waar de grafiek daalt en stijgt moet je zowel links van de 0 als rechts van de nul een getal kiezen en die in de afgeleide invullen. Ook moet je 0 zelf invullen, om te kijken wat de grafiek bij x=0 doet."
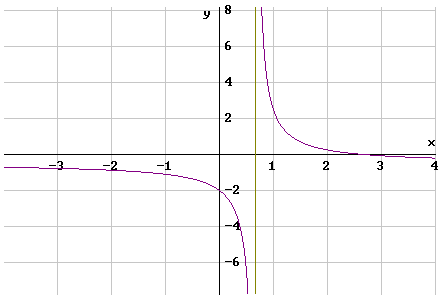
Maar dat klopt niet. Kijk nog 's naar de grafiek. De grafiek daalt overal. Kijk nog 's naar de afgeleide. Met uitzondering van $x$=$\large\frac{2}{3}$ is de afgeleide overal negatief, kleiner dan nul. Dus de grafiek is overal dalend.
Als je 't anders wilt doen kan je ook kijken naar het tekenverloop van de afgeleide. Bereken eerst waar de afgeleide gelijk aan nul is. Dat blijkt nergens het geval te zijn. Je kunt nu links van $x$=$\large\frac{2}{3}$ een punt invullen en constateren dat de afgeleide daar kleiner is dan nul. Je kunt rechts van $x$=$\large\frac{2}{3}$ een punt invullen en constateren dat de afgeleide daar ook kleiner dan nul is, zodat er maar een conclusie mogelijk is: de afgeleide is overal kleiner dan nul. De grafiek is op het domein overal dalend.
Bedoel je dat?
WvR
13-5-2014