WisFaq!

Grafiek tekenen van een differentiaalvergelijking

Beste allen,

Ik zou graag willen weten hoe ik de grafiek van de volgende differentiaalvergelijking in mijn grafische rekenmachine kan tekenen. Ik moet namelijke bewijzen waarom de getekende grafieken geen oplossing van de differentiaalvergelijking zijn. Het gaat om de volgende differentiaalvergelijking:

dy/dt=e^t·(y-1)².

Mario

Mario Leebart
7-3-2014

Antwoord

Er is niet zoiets als de grafiek van een differentiaalvergelijking. Je kunt wel een richtingsveld tekenen en dan oplossingskrommen tekenen. Hieronder zie je daar een voorbeeld van.


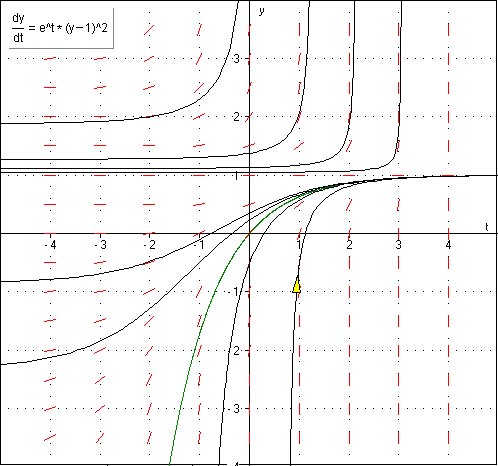
VU-diff

Al die krommen zijn mogelijk oplossingen van de differentiaalvergelijking. Als je goed kijkt staat er ook een groene oplossingskromme bij. Dat is de functie met als voorschrift:

$y=1-\frac{1}{e^{t}}$

Dat is dan één oplossing, maar er zijn er meer. In dit geval kan je die oplossingen zelfs redelijk makkelijk zelf vinden.

Ik begrijp niet helemaal wat je bedoelt met 'bewijzen dat de getekende grafieken' geen oplossing zijn.

Zo'n richtingsveld zit (denk ik) niet ingebouwd in jouw GR. Misschien dat er wel programma's voor zijn, maar 't is misschien handiger om eerst eens precies uit te leggen wat de bedoeling is...

WvR
12-3-2014