WisFaq!

Re: Een machtsfunctie differentiëren

Sorry f(x) was 3^x ik had niet goed gekeken maar ik zie dan dat de rc van de raaklijn -1,1 is in het antwoord moet ik nu weten dat bij a^x de afgeleide gelijk is aan de afgeleide van -(1/a)^x? Of moet ik dit kunnen aantonen?

mo
7-1-2014

Antwoord

Ja zeg...



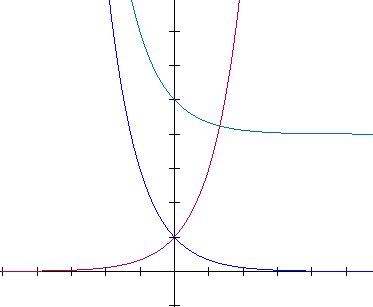
$f(x)=3^{x}$ (rood)
Spiegelen in de y-as!
$h(x)=(\frac{1}{3})^{x}$ (blauw)
Vier omhoog!
$g(x)=(\frac{1}{3})^{x}+4$ (groen)

De raaklijn voor x=0 was bij benadering: $y=1,1x+1$
$y=1,1x+1$
Spiegelen in de y-as!
$y=-1,1x+1$
Vier omhoog!
$y=-1,1x+5$

Mij krijg je niet gek...

Hoe was het ook weer? Spiegelen in de y-as betekent dat je in het functie voorschrift $x$ vervangt door $-x$.

$f(x)=3^{x}$ wordt dan is $h(x)=3^{-x}$
$h(x)=3^{-x}$
$h(x)=(3^{-1})^{x}$
$h(x)=(\frac{1}{3})^{x}$

Zoiets...?

Zie overzicht transformaties van grafieken

WvR
7-1-2014