WisFaq!

Raaklijn van een parametervoorstelling

Hoi,

Hoe vind ik de raaklijn van een parametervoorstelling in een bepaald punt?
De vraag is: gegeven is de parametervoorstelling x = 2(1 + sin at) en y = cos 2t; waarbij a = 4 en een interval van 0
$\le$ t $\le$ 2p
Stel de vergelijkingen op van elk van de lijnen die de kromme in het punt (2,0) raken.

Hoe doe ik dit?

Josefien
9-11-2013

Antwoord

Hoi Josefien,

Wellicht helpt onderstaande wat.

$
\begin{array}{l}
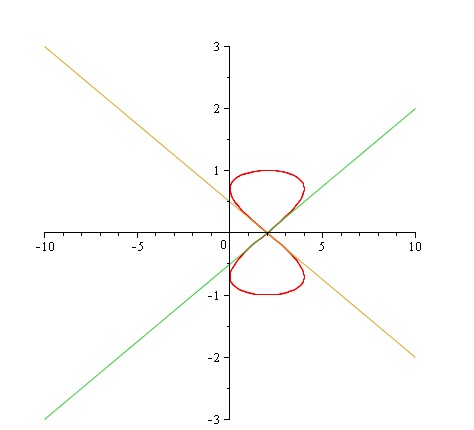
R(t) = \left\{ \begin{array}{l}
x(t) = 2(1 + \sin (4t)) \\
y(t) = \cos (2t) \\
\end{array} \right\} \\
R'(t) = \frac{{y'}}{{x'}} = \frac{{ - 2\sin (2t)}}{{8\cos (4t)}} \\
\left\{ \begin{array}{l}
x = 2 \\
y = 0 \\
\end{array} \right\}t = \frac{1}{4}\pi + \frac{2}{4}k\pi \Rightarrow \frac{1}{4}\pi ,\frac{3}{4}\pi ..... \Rightarrow rc = \frac{{ - 1}}{4},\frac{1}{4} \\
y_1 = \frac{{ - 1}}{4}(x - 2) \\
y_2 = \frac{1}{4}(x - 2) \\
\end{array}
$



mvg DvL

DvL
9-11-2013