WisFaq!

Omwentelingslichaam y-as

Hallo, ik had een vraagje over het berekenen van de inhoud van een omwentelingslichaam rond de y-as, van de volgende functie: f(x)= ��(2x²+2) met het interval [0,7]

Er staat in mijn boek wel een voorbeeld, maar ik begrijp niet hoe ze aan die getallen komen en het dus invullen.
Er staat in het voorbeeld:
f(x)=��(x-1) op het interval [2,10]
y = ��(x-1), dus x-1= y² en x = y²+1, f(2)=1 en f(10)=3
Hoe komen ze hieraan? Ik dacht als ik het voorbeeld begrijp kan ik misschien de 1e functie zelf proberen. Kunt u mij hiermee aub helpen?

Yvette
30-8-2013

Antwoord

Hallo Yvette,
we gaan eens een poging doen.
Allereerst moeten we beseffen dat het omwentelen om de y-as hetzelfde is als de inverse om de x-as. Dit omdat de inverse niet meer is dan een spiegeling in de lijn y=x ( om het te zien moet je de inverse en de orginele maar eens plotten)



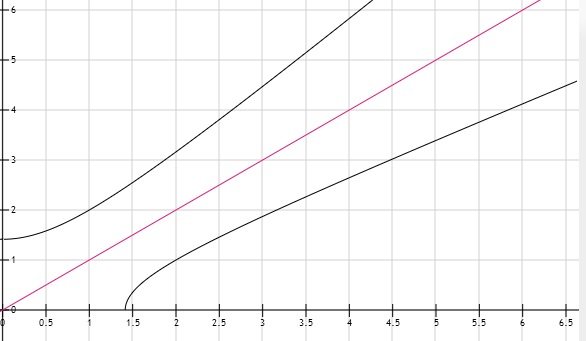
Welnu de inverse functie = y=��((x²-2)/2) ( Ik neem aan dat je weet hoe je een inverse bepaald?)

Het interval voor de omwenteling om de y-as was [0,7] Dit geeft voor de inverse functie het interval [��2,10] Immers bij de orginele functie geldt f(0)=��2 en f(7)=10 ( Omdat je de inverse pakt, moet je deze punten dus ook spiegelen en dus worden de grenswaarde voor de inverse [��,10) ( Zie ook het plaatje als je dit niet meteen volgt).

Goed we hebben nu dus een nieuwe functie met nieuwe grenswaarde waarbij de inhoud van het omwentelingslichaam gelijk is. Dit kun je oplossen met de volgende integraal.

$\pi\int{}$��((x²-2)/2)² = $\pi\int{}$(x²-2)/2) met grenzen ��2,10

Ik neem aan dat die integraal je ook lukt?

Kun je zo verder, anders roep je nog maar eens!

mvg DvL

DvL
30-8-2013