WisFaq!

Eigenschappen bewijzen

Bewijs de volgende eigenschappen:

A) als alle waarnemingen x_i met een positieve factor a worden vermenigvuldigd, dan wordt de standaardafwijking met dezelfde factor vermenigvuldigd.

B) de standaardafwijking verandert niet wanneer bij alle waarnemingen een vast getal b wordt opgeteld.

Deze eigenschappen lijken mij wel logisch, maar ik weet niet hoe ik deze het best kan bewijzen, kan iemand me helpen?

Alvast bedankt!

Ano
2-6-2013

Antwoord

Ga uit van de formule voor de standaardafwijking:



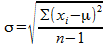
Wanneer je alle waarnemingen met een factor a vermenigvuldigt, dan krijg je een nieuwe serie waarnemingen met waarden a×x_i. De gemiddelde waarde m verandert ook, deze wordt nu a×m. Voor de nieuwe standaardafwijking geldt dan:



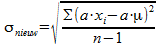
Je moet bewijzen: s_nieuw = a×s

Je moet dus laten zien dat geldt:



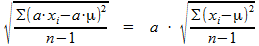
Voor het optellen met een vaste waarde b volg je eenzelfde soort redenering: alle x_i worden vervangen door (x_i+b). Vervang het gemiddelde door het nieuwe gemiddelde (kan je zelf afleiden wat het nieuwe gemiddelde wordt?). Uiteindelijk moet je aantonen:



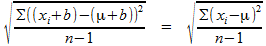
Gaat het hiermee lukken?

GHvD
2-6-2013