WisFaq!

Pythagoreische drietallen

Hallo

Een bijzondere formule voor pythagoreische drietallen is de volgende. Bij twee opeenvolgende oneven getallen bijv. 7 en 9. Neem de som van hun omgekeerde dus:

1     1     16 -  +  -  =  -- 7     9     63  

Dan zijn 16 en 63 de twee rechthoekzijden van een rechthoekige driehoek, want:
16² + 63² = 65²

Dan moet ik zonder voorbeelden aantonen dat deze formule geldt voor elk twee-tal opeenvolgende oneven getallen dus n-1 en n+1 met n een even getal

alvast bedankt

Niels
28-1-2003

Antwoord

Het is een kwestie van optellen van niet-gelijknamige breuken. Als jij goed begrijpt wat er hieronder gebeurt met jouw voorbeeld:



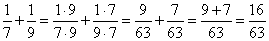
dan zal je dit ook zo kunnen berekenen met de getallen n-1 en n+1, de eerste stap is:



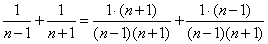
Je krijgt er dan uit dat de getallen 2n en (n-1)(n+1) de lengtes van rechthoekszijden zijn van een rechthoekige driehoek met een schuine zijde van n²+1.
Dit kun je gewoon narekenen door de stelling van Pythagoras toe te passen en alle haakjes netjes uit te werken.
Ik laat dat aan jou over.

jr
28-1-2003