WisFaq!

Raaklijn aan parameterkromme

Ik moet de raaklijn aan een parameterkromme kunnen berekenen.

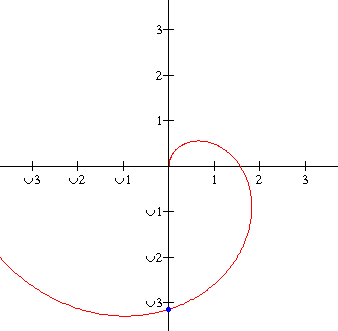
Bijvoorbeeld de raaklijn aan deze kromme in punt P(0,-$\pi$):

x= t sin t
y= t cos t

Ik zou op basis van de coördinaten van het punt P eerst de waarde van t moeten berekenen denk ik, om die waarde dan in te vullen in de afgeleide van de parameterkromme om de rico van de raaklijn uit te komen.

Die rico zou 1/$\pi$ moeten zijn, maar ik snap niet hoe je dat kan uitkomen. Want als je voor x een 0 invult, zou t ook 0 moeten zijn. En dat kan volgens mij niet, want dan klopt het toch niet voor y=-$\pi$?

Kunnen jullie mij op weg helpen?

joeri
21-4-2013

Antwoord

Als x=0 dan is t=0 of sin t=0. Als t=0 kan y niet -$\pi$ zijn, dus dan zal sin(t)=0 moeten zijn. Dan kan voor (bijvoorbeeld) t=$\pi$ en dan klopt het precies.

x = $\pi$ · sin $\pi$ = 0
y = $\pi$ · cos $\pi$ = -$\pi$



Zou het lukken?

Zie ook 2. Raaklijnen

WvR
21-4-2013