WisFaq!

Asymptoten

Ik heb de functie 20/8x²-32,daarvan moet ik de asymptoten berekenen. Mijn stappen die ik zelf genomen heb, (als ik dat goed gedaan heb, is het ontbinden van de formule.)
Dus 5/2(x²-8) = 5/2(x²-4) = 5/2(x-2)·(x+2) alleen nu loop ik vast, hoe moet ik verder om de asymptoten te berekenen? (Ik heb moeite als er een kwadraat in staat).

Yvette
17-4-2013

Antwoord

Mogelijke kandidaten voor een vertical asymptoot kan je vinden waar de noemer nul is en de teller niet.

$
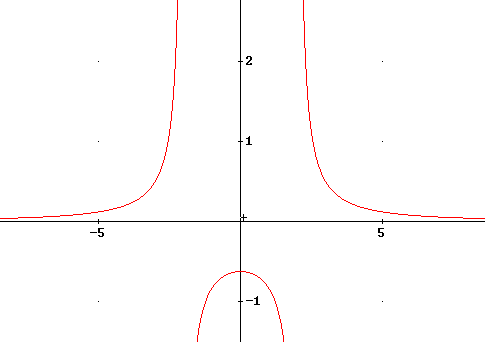
\Large f(x) = \frac{{20}}{{8x^2 - 32}} = \frac{{20}}{{8(x^2 - 4)}} = \frac{5}{{2\left( {x - 2} \right)\left( {x + 2} \right)}}
$

Dus dat klopt wel en dat geeft $x=-2$ en $x=2$ als verticale asymptoten.

Voor de horizontale asymptoten kan je delen door de grootste macht van $x$. Dat geeft bijvoorbeeld:

$
\Large \mathop {\lim }\limits_{x \to \infty } \frac{{20}}{{8x^2 - 32}} = \mathop {\lim }\limits_{x \to \infty } \frac{{\frac{{20}}{{x^2 }}}}{{8 - \frac{{32}}{{x^2 }}}} = 0
$

WvR
18-4-2013