WisFaq!

Cardano bijna ontrafeld

hallo,

wij hebben als onderwerp voor onze wiskunde PO de formule van cardano. de formule is ons bekend, aangezien die op vele sites staat, maar wij willen zelf tot de formule komen aan de hand van deze site http://thesaurus.maths.org/dictionary/map/word/621
Wij hebben tot nu toe alles stappen kunnen herleiden alleen we blijven steken op het einde. u^3 kunnen we berekenen en dus vervolgens ook u.

u=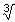((-q+(q²+(4/27)p³)):2) OF
u=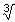((-q-(q²+(4/27)p³)):2)

Nu staat er op die site dat je nu ook v kunt vinden, omdat v=(p/(3u)). Maar we hebben nu 2 verschillende u's, omdat je de oplossing van een kwadratische vergelijking zoekt en dat zijn meestal 2 mogelijkheden. En als we nu 1 van de 2 u's invullen in v=(p/(3u)), dan krijg je een hele rare deling met p.

Dus nu is onze vraag: Hoe zit het met de 2 verschillende u's en hoe kunnen we tot v komen. De laatste 2 stappen nml, y=u-v en als laatst x=y-(b/(3a)) zouden geen probleem meer moeten zijn als we u en v weten.

Alvast bedankt,

Maarten en Jordy

Maarten en Jordy
19-1-2003

Antwoord

Beste Maarten en Jordy,
Een hele klus het ontrafelen van Cardano. Maar dapper van jullie.
Als ik het goed begrijp vallen jullie over het feit dat bij:
(u³)²+qu³-p³/27=0
Als we even u³ vervangen door g, ofwel stellen g = u³, dan krijgen we zo de vergelijking:
g²+qg-p³/27 = 0
En aangezien q en p reeds te berekenen zijn is dit inderdaad een 2e graads vergelijking, die ook twee antwoorden zal opleveren. Maar let op, het worden er meer dan 2, want er geldt niet u = uitkomst 2e graads maar u³ is hierhaan gelijk.
Je krijgt indien je g berekend voor u dus drie antwoorden per gevonden g. Ofwel je krijgt er al 6 in totaal. Echter je zal merken dat 3 hiervan steeds op het eind gelijk worden. Waarom dit weer is, is vrij lastig, en zal ik jullie eerst mee laten ploeteren

Hopelijk is jullie vraag zo voldoende beantwoord.
Eventueel een uitgebreide uitwerking is te vinden op onderstaande link

M.v.g.

Zie Website van P.H. Stikker [http://home.uwnet.nl/~stikpet/PHStikker/CardanoOplossing.pdf ]

PHS
20-1-2003