WisFaq!

Maximale manteloppervlakte van een omwentelingskegel aan een halve bol

Een omwentelingskegel is omschreven aan een halve bol met straal r. Het grondvlak van de kegel ligt in het vlak dat de halve bol begrenst. Bepaal de straal en de hoogte van de kegel waardoor de manteloppervlakte maximaal wordt.

Eddy Raymaekers
11-2-2012

Antwoord

Hallo

De manteloppervakte van een kegel is gelijk aan $\pi$.R.a
waarbij R (straal van het grondvlak) = |AC| en a (apothema) = |BC|
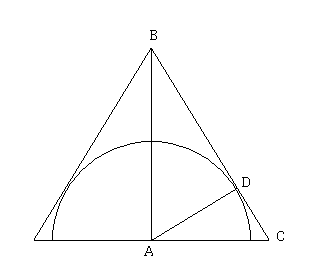
op de onderstaande tekening van de vlakke doorsnede.

We nemen R = x als veranderlijke, dus moeten we a uitdrukken in functie van R en r (straal van de halve bol).

De driehoeken $\Delta$ABC en $\Delta$DAC zijn gelijkvormig.
Hieruit vind je een verband tussen R=|AC| , a=|BC| , |AB| en r=|AD|
en |AB|² = |BC|² - |AC|²
Dus kun je nu a uitdrukken in functie van R en r .

Bepaal nu het maximum van deze functie.
Ok?

Je vindt : R = r.√(³/₂)

LL
12-2-2012