WisFaq!

Hypotheek - Annuiteiten

Voor een werkstuk voor school,moeten wij enkele vragen over een Annuiteiten-Hypotheek beantwoorden. Bij Lennart van Loon( op 7-5-2002 ),werd dit al kort beantwoord. Maar, wij wilden eigenlijk vragen, hoe DE bank,bij het opstellen van een Annuiteit de Wiskunde gebruikt. Hoe komt de Bank bijvoorbeeld aan een vast bedrag van 5000 Euro per maand?
Onze vraag is dus eigenlijk : " Hoe wordt zo`n Annuiteiten-hypotheek vast gesteld door de bank,en bestaat daar een algemene formule voor,die ze daarbij gebruiken ?" Ze komen niet zomaar aan een bedrag per maand.
Groeten,
Remco & Marcel.

Remco & Marcel
14-1-2003

Antwoord

Op zich ben je al vrij ver met de antwoorden hier op Wisfaq over Annuïteiten (en ook de vele voorbeelden in de rubriek economisch). Want op zich is dat allemaal juist hetzelfde als vanuit het standpunt van de bank. Het gaat voor beide partijen immers om hetzelfde bedrag van de lening, dezelfde intrest, dezelfde looptijd en dezelfde aflossingen. Enig verschilpunt is dat het bij het standpunt van de bank de tekens van de bedragen allemaal tegengesteld zijn. Op zich moet je daar niet naar kijken, want in een wiskundige betekenis maakt dat weinig verschil. Dit verschil komt doordat men als men 100% correct wil zijn een positief teken neemt als men geld krijgt en een negatief teken als men geld geeft. Als een bank € 10.000 geeft is dit negatief vanuit het standpunt van de bank, maar positief voor de gebruiker. In de formules die gaan komen, mag je dit aspect verwaarlozen (houd het enkel in je achterhoofd).

Nu: er is inderdaad een wonderformule voor de bank om onmiddellijk het juiste bedrag van de aflossing te bepalen, alleen als je die formule ziet, word je gewoonweg ziek (5 regels lang met ongeveer 20 variabelen). Ik zal ze niet geven, want ik ben bang dat er enkele wiskundige begrippen in staan die jullie misschien niet kennen. Om jullie gerust te stellen: ik denk niet dat ze in de praktijk gebruikt wordt. Banken maken enkele vereenvoudigingen, waarbij het resultaat toch vrij dicht bij de formule aansluit.

Hypotheken hebben eigenlijk heel veel met wiskunde te maken. 2 begrippen zijn van belang: intresten en rijen.

De herkomst van volgende fomule staat uitgebreider te vinden op de link onderaan.

Slotwaarde = a + a.(1+r) + a.(1+r)² + … + a.(1+r)^n-1

= a. [1 + (1+r) + (1+r)² + … + (1+r)^n-1]

met a = jaarlijkse aflossing
r = intrestpercentage
n = termijn

Gebruik makend van de eigenschappen van een meetkundige rij kunnen we dit herschrijven als:



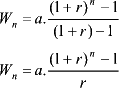
In de praktijk worden lening echter niet per jaar afbetaald, maar per maand. De formule wordt dan aangepast door n te vervangen door 12n, r door p (maandelijks percentage) en a door M (maandelijkse aflossing). Banken gaan vaak nog een stapje verder door te rekenen met dagen (maar de aflossing blijft per maand = 30.M). Opmerking: voor de bank telt elke maand 30 dagen en een jaar 360 dagen.

Ik denk dat jullie de nodige aanpassingen wel verder kunnen doen. Ik geloof dat jullie voornamelijk geïnteresseerd waren in hoe de bank de maandelijkse aflossing bepaalt. Wel: die heb je nu. Gewoon de formule herschrijven naar M.

Enig probleem: je kent de waarde van de slotwaarde niet. De bovenstaande methode was goed om het principe uit te leggen en wordt het meest gebruikt. Nu er is ook een formule voor de beginwaarde (= geleend bedrag) waar M ook in staat als enige onbekende. De formule vind je wel in de vragen op Wisfaq.

Nog enkele slotopmerkingen. We hebben nu een maandelijkse aflossing die steeds constant is (wat voldoende is voor een werkstuk). Er zijn 2 alternatieven: een stijgende en dalende aflossing. Ook hebben we genomen dat er steeds op het einde van de maand betaalt wordt (postnumerando), terwijl dit vaak in het begin van de maand is (prenumerando). Je kan het resultaat van deze aanpassingen vinden door de formule van de rij aan te passen aan de nieuwe omstandigheden en zo tot een nieuwe formule komen. Op onderstaande link staat een bestand met een korte uitleg bij enkele belangrijke begrippen uit de financiële economie (voornamelijk betreffende annuïteiten).

Dit is zowat de basis die banken gebruiken voor de berekening. Ze kennen echter deze formules niet zo, omdat die in hun computerprogramma's zitten (misschien iets verfijnder dan hier, maar onze werkwijze benadert het heel goed). Ook op internet vind je enkele van deze programmaatjes (zoek maar eens op Hypotheek berekenen). Banken houden voor de rest nog rekening met enkele menselijke aspecten, zoals leeftijd, inkomen, gezondheid en passen desnoods de looptijd aan. Maar deze laatste elementen dienen niet echt uitgewerkt te worden voor jullie werk.

Ik hoop dat ik jullie een goed beeld heb gegeven van het wiskundig mechanisme hierachter en stel gerust nog vragen als je er nog zou hebben.

Groetjes,

Tom

Zie Tijdswaarde van geld [http://users.skynet.be/crohn/wisfaq/wisfaq.htm]

tg
16-1-2003