WisFaq!

Inhoud gedeelte van een bolsegment

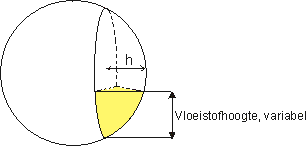
Hoe bereken ik de inhoud van dit gedeelte van een bolsegment?

Ceulemans Etienne
19-11-2001

Antwoord

Hierbij een manier om de inhoud numeriek te benaderen met een integraal.



x is de vloeistofhoogte, gemeten vanaf de onderkant van het bolsegment.
R is de straal van de bol.
r is de staal van de cirkel van het bolsegment zelf.
z is de straal van de cirkel die de horizontale doorsnede vormt van de bol op hoogte x.
Er geldt dan:
y=√(2rx-x²)
z=√(R²-(r-x)²)
Voor de oppervlakte van de vloeistof op hoogte x geldt dan:
opp(x)=arcsin(y/z)·z²-z²·sin(2arcsin(y/z))/2
Deze oppervlakte integreren van 0 tot de hoogte geeft de inhoud. Analytisch integreren valt niet mee, maar numeriek kom je een heel eind.

Anneke
26-3-2003