 ):
): 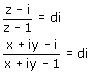
..en dan zou het moeten lukken.
WvR
6-1-2003
Toon aan dat alle complexe getallen z waarvoor (z-i)/(z-1) zuiver imaginair is , op een unieke cirkel liggen. Bepaal middelpunt en straal van die cirkel. Je moet een substitutie doen van z=x+iy zodat de teller van het reeele gedeelte x²+y²-x-y is, middelpunt en straal van de gevraagde cirkel bepalen is een makkie dan , maar hoe kom je aan die vergelijking?Berten
6-1-2003
Vul in z=x+iy en je weet dat er iets uit moet komen als di (met dÎ):
..en dan zou het moeten lukken.
WvR
6-1-2003
#6391 - Complexegetallen - 3de graad ASO