WisFaq!

Periodieke functies

Hallo, ik moet voor een taak oefeningen uit m'n boek maken, maar ik weet echt niet hoe het moet:

Voor een bepaalde stad worden de gemiddelde dagtemperaturen gegeven door het verband:

$
\eqalign{\theta (t) = 20 \cdot \sin \left( {\frac{{2\pi }}
{{365}}\left( {t - 120} \right)} \right) + 5}
$

...met $\theta$ in °C en $t$ in dagen, $t$ is een element van (0,365). Het groeiseizoen rond die stad bestaat uit de dagen met een gemiddelde dagtemperatuur van minstens 5°C.

1. plot de grafiek van $\theta$
2. maak gebruik van de grafiek van $\theta$ om het begin en het einde van het groeiseizoen bij benadering te bepalen
3. bereken het begin-en het eindtijdstip van het groeiseizoen met behulp van een goniometrische vergelijking

Ik hoop dat iemand mij kan helpen!?!
Alvast bedankt,
Eva

Eva
16-10-2010

Antwoord

De opdracht 'plot' suggereert dat je de grafiek mag plotten met je grafische rekenmachine. Mocht dat niet het geval zijn dan kan je wel een schets maken. Op Periodieke functies kan je daar meer over vinden.

De grafiek van opgave 1 ziet er dan zo uit:



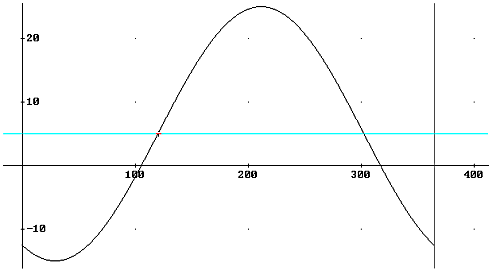
Met de plot van je GR of je schets kan je aflezen dat na 120 dagen de temperatuur voor 't eerste boven de 5° uitkomt.

Je kunt dat de grenzen ook berekenen met:

$
\eqalign{
& 20 \cdot \sin \left( {\frac{{2\pi }}
{{365}}\left( {x - 120} \right)} \right) + 5 = 5 \cr
& 20 \cdot \sin \left( {\frac{{2\pi }}
{{365}}\left( {x - 120} \right)} \right) = 0 \cr
& \sin \left( {\frac{{2\pi }}
{{365}}\left( {x - 120} \right)} \right) = 0 \cr
& \frac{{2\pi }}
{{365}}\left( {x - 120} \right) = 0 \vee \frac{{2\pi }}
{{365}}\left( {x - 120} \right) = \pi \cr
& x - 120 = 0 \vee x - 120 = 182,5 \cr
& x = 120 \vee x = 302,5 \cr}
$

WvR
16-10-2010