WisFaq!

Kansen voor een schakelaarsysteem

Ik heb twee schakelingsystemen en moet bepalen welk systeem beter is, dus een kleinere kans op falen heeft.
Beide systemen hebben 4 schakelaars A,B,C en D. Verder is gegeven dat de kans dat een schakelaar werkt gelijk aan p is. A en B zijn parallel aan elkaar geschakelt en C en D. Het systeem werkt als A of B werkt en C of D werkt. Dus in verzameling notatie:

(A$\cup$B)$\cap$(C$\cup$D)

Ik weet hoe ik hier verder moet om de kans uit te kunnen rekenen, bij dit systeem. Maar ik heb nog een tweede systeem waar gegeven is dat het systeem werkt als minstens twee van de 4 schakelaars A, B, C en D werken. Ik moet een zelfde soort uitdrukking in verzameling notatie als bovenstaande. Omdat ik later ook moet conditioneren verder in de som als de componenten afhankelijk van elkaar zijn.

(A$\cap$B)$\cup$(A$\cap$C)$\cup$(A$\cap$D)$\cup$(B$\cap$C)$\cup$(B$\cap$D)$\cup$(C$\cap$D)

Maar ik denk niet dat dit klopt, zit bijv. de kans dat alle schakelingen werken hierin verwerkt?
Hoop dat u mij kunt helpen om de juiste uitdrukking te verkrijgen.

Groeten,

Stewart

Stewart
21-9-2010

Antwoord

Hallo

We kunnen de 2 schakelingen (ik noem ze S1 en S2) voorstellen met de volgende Booleaanse uitdrukkingen:
S1=(A+B).(C+D) = A.C + A.D + B.C + B.D
S2 = A.B + A.C + A.D + B.C + B.D + C.D
waarbij
"+" staat voor "of" (parallelschakeling) en
"." staat voor "en" (serieschakeling)

Er zijn 16 mogelijke standen voor de vier schakelaars, die in een waardetabel kunnen worden weergegeven. Voor iedere mogelijkheid staat telkens de kans op deze schakeling, waarbij p de kans is dat een schakelaar gesloten is.



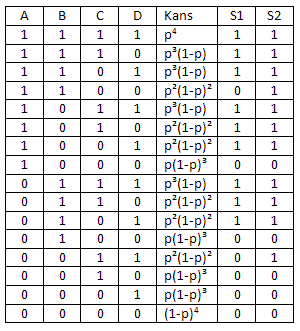
(Ik veronderstel dat je bedoelt :
"de schakelaar werkt" = "de schakelaar is gesloten")
Ook is de waarde van de twee schakelingen S1 en S2 weergegeven, met "1" = de schakeling werkt, en "0" de schakeling werkt niet.
De kans dat S1 werkt is dan de som van de afzonderlijke schakelingen dat S1 werkt en is dus gelijk aan :
P(S1) = p⁴ + 4.p³(1-p) + 4.p²(1-p)² = p²(p²-4p+4)
En zo is
P(S2) = p⁴ + 4.p³(1-p) + 6.p²(1-p)² = p²(3p²-8p+6)

Als bijvoorbeeld p=0.5, dan P(S1)=0.5625 (=⁹/₁₆) en P(S2)=0.6875 (=¹¹/₁₆)
Met p=0.7, geldt P(S1)=0.8281 en P(S2)=0.9163
Met p=0.3, geldt P(S1)=0.2601 en P(S2)=0.3483

LL
26-9-2010