WisFaq!

Oppervlakte

Hallo Wisfaq-team,
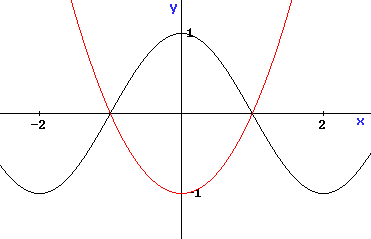
De grafiek van de functies f(x)=cos($\pi$/2·x) en g(x)= x²-1
zijn gegeven.
Vraag: bereken de oppervlakte ingesloten door beide krommen...

Antwoord:(12+4[$\pi$])/3$\pi$

Ik maak dus de aftrekking f-g =0
cos($\pi$/2)x-x²+1=0 Ik probeer de grenzen te vinden en dat lukt mij niet evenmin als het tekenonderzoek.
-x²+cos($\pi$/2)x+1=0 geeft met cos$\pi$/2=0 een wortel x=-2
Dit is een grenspunt, waar vind ik het anderen om te kunnen integreren en de oppervlakte te berekenen?
de geintegreerde functie is, denk ik toch:
I= -x³/3+(2/$\pi$sin($\pi$/2)x)+x+C
Vriendelijke groeten

Rik Lemmens
5-8-2010

Antwoord

De grafieken van f en g snijden elkaar in (-1,0) en (1,0). Zoiets kan je 'bedenken' als je de grafieken van beide functies even schetst. Je kunt ze natuurlijk ook even plotten met de grafische rekenmachine of een programma:



Daarna kan je natuurlijk nog wel even controleren of dat ook echt klopt en dat klopt!

Daarna zal het wel lukken, denk ik...

WvR
6-8-2010