WisFaq!

Driehoek en negenpuntscirkel

Gegeven een scherphoekige driehoek met een tophoek van 60 graden. Hoe bewijs ik in dit geval dat het middelpunt van de negenpuntscirkel op de bissectrice van die tophoek ligt?

g.jacobsen
25-1-2010

Antwoord

Zoals bekend is het middelpunt N van de negenpuntscirkel het midden van het lijnstuk OH (H is hoogtepunt en O is middelpunt van de omcirkel van ABC).
D, E, F zijn de voetpunten van de hoogtelijnen; K, L, M zijn de middens van de zijden. En deze 6 punten liggen op de negenpuntscirkel.

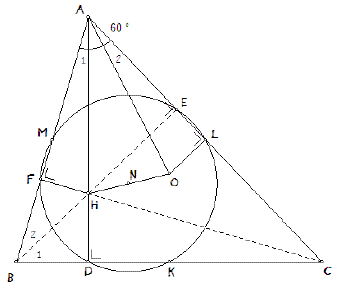
In driehoek BEA is B2 = 30º, dus HF = ¹/₂BH. Maar ook OL = ¹/₂BH (een eigenschap van het punt O), zodat OL = HF.
Verder is in driehoek BDA: A1 = 90º - B, en in driehoek ALO is AOL = B (halve middelpuntshoek), zodat A2 = 90º - B.
De driehoeken AFH en ALO zijn daarmee congruent (ZHH).
Driehoek OAH is dus gelijkbenig, en dan ligt het punt N op de bissectrice van OAH, en omdat A1 = A2 dus ook op de bissectrice van CAB.

dk
26-1-2010