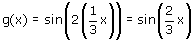Ik ben op zoek naar een (ingewikkelde?) expliciete functie (y= ...) waarbij ik meerdere basisfuncties moet combineren met volgende combinaties:
- Optellen/aftrekken
- Vermenigvuldigen
- Verschuiving (X & Y richting)
- Spiegelen
- |...| (absolute waarden nemen)
Met de nieuwe opgebouwde functie zouden deze combinaties goed te illustreren zijn.
Nu heb ik al vanalles geprobeerd maar ben van sommige dingen niet zeker:
- Als je nu de functie y = x + 4 hebt dan verschuift de functie 4 eenheden naar boven maar dit zijn toch wel degelijk 2 functies namelijk y = X en y = 4?
- Ik had dan iets gevonden in de vorm van y = e^(1/X2)*abs(Sin(x))+4 maar hoe kan ik deze functie spiegelen en hoe kan ik deze verschuiven in de X richting? want wanneer X=0 is er een verticale asymptoot aanwezig. Is de raaklijn is x=0 dan onbestaand of is dit gelijk aan de verticale asymptoot?
- (Hoe zouden jullie deze oefening het best aanpakken?)
Alvast HARTELIJK bedankt

Marnik
Marnik Van Hileghem
6-1-2010
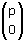 vervang je 'x' in het functievoorschrift door 'x-p'.
vervang je 'x' in het functievoorschrift door 'x-p'.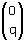 tel je q op bij het functievoorschrift.
tel je q op bij het functievoorschrift.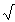 x-4 over de vector
x-4 over de vector  . Geef het functievoorschrift van g.
. Geef het functievoorschrift van g.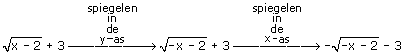
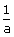 ·x
·x