We beginnen met :
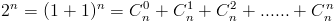
en dus ook :
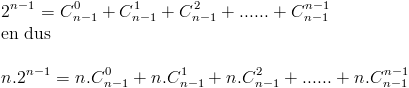
We moeten nu bewijzen dat :
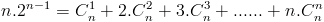
We bewijzen nu dat de overeenkomstige termen in deze twee reeksen gelijk zijn, bijvoorbeeld :
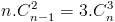
Het algemene bewijs :
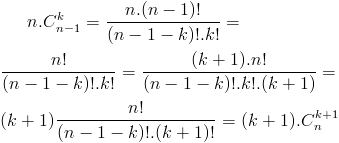
Lukt het zo?
LL
23-11-2009
Was dit niet het principe van de vorige oefeninge?
dat bewijs snapte ik volledig, daar was het gelijkgesteld aan: (-1)^n dus pas je toe wat jij zegt, maar nu is het een andere oefening die ik ook moet bewijzen en daar is:
C(1/n) + 2C(2/n) + 3C(3/n) +...+ nC(n/n) = n.2^(n-1)
hier kunnen we toch moeilijk -1 vervangen door 2- 1 want hier komt geen '-1' in voor :s
met vriendelijke groeten.Shari Leysen
23-11-2009
Je hebt gelijk, ik dacht inderdaad dat het nog over de vorige oefening ging.
We beginnen met :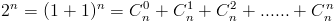
en dus ook :
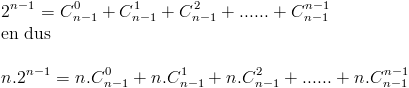
We moeten nu bewijzen dat :
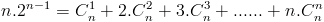
We bewijzen nu dat de overeenkomstige termen in deze twee reeksen gelijk zijn, bijvoorbeeld :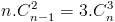
Het algemene bewijs :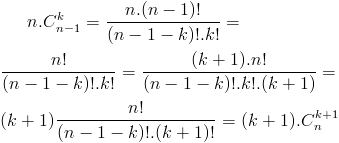
Lukt het zo?
LL
23-11-2009
#60859 - Kansrekenen - 3de graad ASO