WisFaq!

Re: Methode van Newton raphson

Ai ik lijk er nog niet aan uit te kunnen, hoe bewijs je dan dat er meerdere start oplossingen zijn, dus meerdere x₀? want jij besluit dat er maar 1 is, de 4.4934 (hoe kom je hier trouwens aan?) , maar naar het schijnt zijn er zelfs oneindig veel nulpunten, maar hoe je dat moet weten, weet ik niet..
en de oefening zelf,hoe moet ik verder na die tanx = x ?

met vriendelijke groeten

Shari Leysen
3-10-2009

Antwoord

De methode van Newton-Raphson? Moet je dan niet zoiets als dit doen:

$
\LARGE x_{n + 1} = x_n - {{f(x_n )} \over {f'(x_n )}}
$

Bij verschillende waarden voor x₀ krijg je mogelijk benaderingen voor verschillende nulpunten. Het is misschien zelfs mogelijk dat het helemaal niet werkt!

f(x)=sin(x)-x·cos(x)
f'(x)=x·sin(x)

Als je dan x₀=4,712 neemt kom je vrij snel uit op een benadering voor een nulpunt x=4,4934. Zoiets gaat handig met de grafische rekenmachine:



Dat er meerdere oplossingen zijn volgt uit sin(x)-x·cos(x)=0. De vergelijking oplossen gaat niet 'echt'. Logisch, want anders hadden we die Newton-Raphson helemaal niet nodig.

sin(x)-x·cos(x)=0
x·cos(x)=sin(x)
x=$\frac{sin(x)}{cos(x)}$
x=tan(x)

Daar heb je toch wel iets aan, want als je de grafiek van y=x en y=tan(x) even voorstelt dan kan je wel 'inzien' dat er oneindig veel oplossingen zijn:



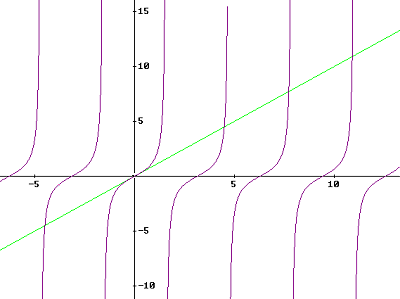
Hopelijk geeft dit voldoende aanknopingspunten voor de rest van de opdracht. Succes!

Zie ook:

• Newton en Raphson
• Re: Newton-Raphson
• Newton-methode op grafische rekenmachine

Zie Wikipedia | Newton-Raphson [http://nl.wikipedia.org/wiki/Newton-Raphson]

WvR
4-10-2009