WisFaq!

Hoe teken je in Cabri II of II Plus een raaklijn aan een grafiek?

Als je in Cabri II Plus naar de 'Assistant' gaat en vervolgens naar 'My classroom' en dan 'Functions and graphs' laten ze de constructie van de afgeleide functie zien. Daarbij maken ze bij de constructie gebruik van de raaklijn. Hoe krijg ik die op mijn scherm?

irene corbet
9-7-2009

Antwoord

Dag Irene,

Allereerst, als je in staat bent de 'Assistant' (ook wel 'Compagnon') te laden, dan staat (ergens) op je eigen systeem het Cabri-bestand '1-graph_dydx.env'.
Als je dat bestand in Cabri II Plus laadt, zou je in staat moeten zijn via 'Herhaal constructie' de opbouw van eea. te zien.
(Rechts naast het plaatje, na laden, staat een aantal verborgen objecten. Maak die eerst zichtbaar!)

In onderstaande figuur (niet dynamisch) zie je iets dergelijks.



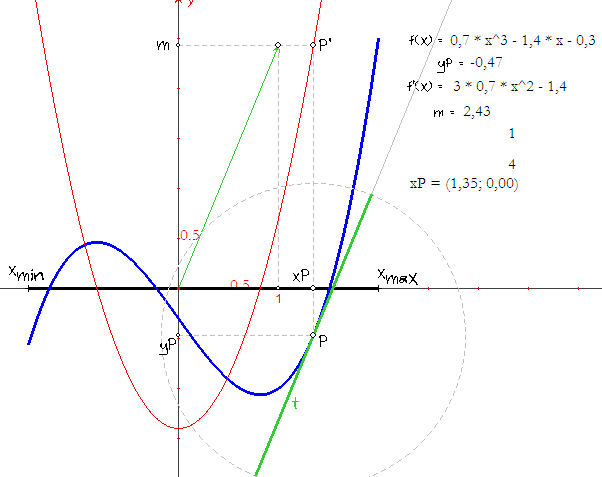
We gaan uit van de expressies:
0,7 · x³ - 1,4 · x - 0,3; dat is het functievoorschrift van f(x)
en:
3 · 0,7 · x² - 1,4; dat is het functievoorschrift van f '(x).
De functie f is gedefinieerd op het interval [xmin, xmax]; en f ' dus ook. Op het lijnstuk op de x-as dat dat interval bepaalt, ligt het willekeurige punt xP.
De waarde van yP kan je berekenen met 'Bereken expressie' (bij f(x) via de x-coördinaat van xP).
Dan is de meetkundige plaats van het punt (xP, yP) te vinden: dat is de grafiek van de functie f (het punt P is dan het variabele punt op de grafiek van f dat bepaald wordt door xP).
Met de waarde van xP is via de expressie voor f '(x) de rico m van de raaklijn t in P aan de grafiek te vinden (ook weer met 'Bereken expressie' maar nu via de expressie voor f ').
Het punt (1, m) dient als eindpunt van de vector die de richtingsvector is van die raaklijn.
Het getal 1 moet dan eerst op de x-as worden overgebracht (met 'Maat overbrengen').
De lijn door P evenwijdig met die vector is dan de bedoelde raaklijn.
Het getal 4 is de straal van een cirkel om P waarmee je, in plaats van de raaklijn, een raaklijnstuk kunt tekenen.
Het punt P' heeft coördinaten (xP, m). Dat is dus een punt van f '(x).
De meetkundige plaats van P' (met punt xP weer als 'sturend' punt van die MP) is dus de grafiek van de grafiek van f '.

Opmerkingen.
1. Het bovenstaande geldt alleen voor Cabri II Plus (voor Cabri II gaat eea. niet analoog).
Nb. Bestanden met extensie '.env' zijn alleen te laden met Cabri Plus.
2. Je kan de 'raaklijn' ook vinden via de lijn door (xP, yP) en (xP', yP') waarbij xP' = xP + h (met bijvoorbeeld h = 0,001) en yP' = f(xP'). Het is dan weliswaar een benadering, maar het werkt wel goed.

Ik hoop dat het bovenstaande voldoende aanwijzingen bevat. En zo niet, je weet ons te vinden!

dk
10-7-2009