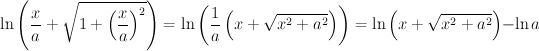WisFaq!

Een standaard integraal afleiden

In een schoolopgave had ik een standaardintegraal nodig, die we nog niet geleerd hadden en ook niet voorkwam in de lijst met formules etc. Het betreft: Int {1/Ö(a² + x²)}dx = ln|x + V (a² + x²)| + C. Wel hebben we geleerd:
Int {1/ V (1+ u²)} du = ln (u + Ö(1+u²) + C. Hiervan uigaande heb ik zelf geprobeerd het bewijs te vinden als volgt: Int {1/ Ö(a² + x²)} dx Teller en noemer vermenigvulgd met 1/a; Int [(1/a)/V{(a² + x²)/a²}] dx=
1/a Int[ 1/{1 + (x/a)²}] dx. Stel u = x/a, du = d(x/a)= 1/a dx. Zodat: Int [1/V{1+(x/a)²}] d(x/a)= ln[x/a+Ö(1+(x/a)²] + C. Nu blijkt tot mijn niet geringe teleurstelling dat in het antwoord tweemaal x/a voorkomt, hetgeen niet juist is met de tabel integraal! Wie kan mij vertellen wat er mis gegaan is? Bij voorbaat hartelijk dank.

Johan uit de Bos
22-6-2009

Antwoord

Beste Johan,

Je oplossing is ook goed, hetgeen je kan controleren door terug te differentiëren. Je kan dit ook zo inzien, herschrijf als volgt:



Op het einde gebruik ik ln(x/y) = ln(x)-ln(y). Die ln(a) is een constante en kan dus bij de integratieconstante genomen worden.

mvg,
Tom

td
23-6-2009