De vraag is dan wat moet je dan voor a en b moet nemen zodat het allemaal een beetje gaat passen...

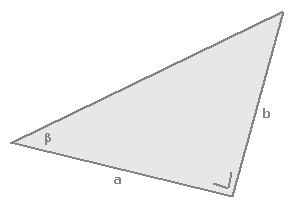
Dan volgt:
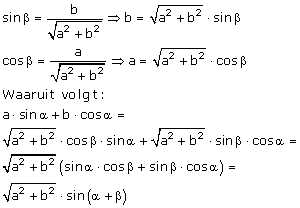
Dus 't is waarschijnlijk eenvoudiger dan je dacht.
WvR
22-5-2009
Ls,
Ik zit met het volgende probleem. De oplossing van de differentiaal vgl van een onderkritisch gedempt systeem is in de vorm:
u(t) = AĚSin(wt) + BĚCos(wt).
Ik heb vernomen dat dit uit te schrijven is als:
u(t) = Í(A2+B2)ĚSin(wt+Phi)
Met Phi gewoon een hoekverdraaing.
Ik kom er alleen maar niet achter hoe dit wiskundig gezien te bewijzen is. Ik heb al geprobeert het uit te schrijven mbv.
Sin(wt) = (e^(wti)-e^(-wti))/(2i)
Cos(wt) = (e^(wti)+e^(-wti))/(2)
Maar het lukt me voor alsnog niet.
Ik hoop dat u me kunt helpen.
Bij voorbaat dank voor uw tijd en met vriendelijke groeten,
DavidDavid
22-5-2009
Feitelijk komt het er op neer dat je aĚsina+b.cosa graag zou willen schrijven als sinaĚcosb+cosaĚsinb. Dat is handig want die laatste uitdrukking is gelijk aan sin(a+b).
De vraag is dan wat moet je dan voor a en b moet nemen zodat het allemaal een beetje gaat passen...
Dan volgt:
Dus 't is waarschijnlijk eenvoudiger dan je dacht.
WvR
22-5-2009
#59379 - Goniometrie - Student universiteit