WisFaq!

Ingeschreven cirkel in rechthoekige driehoek

Ik heb een rechthoekige driehoek, waarvan ik slechts een hoek ken, hoek C: 90 graden. Beide andere hoeken ken ik niet. Daarnaast weet ik de lengte van de overliggende zijde van de rechte hoek (c is de schuine zijde), die lengte is 403. Verder weet ik dat in de ingeschreven cirkel een straal heeft van 74. Door Pythagoras weet ik dat c²=a²+b². Hoe kom ik achter a en b?

Ik ben benieuwd naar de manier van berekenen, ik kan dan eventueel zelf de uitkomst bepalen.

Bram Biegstraaten
25-1-2009

Antwoord

Eerst maar even een tekening:



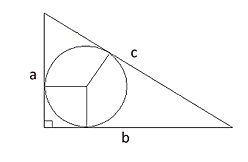
De raakpunten verdelen de zijden in zes stukken, waarvan de stukken met hetzelfde hoekpunt paarswijs even lang zijn. Dus c = (a-r)+(b-r), zodat:

$
\eqalign{c = (a - r) + (b - r) \Rightarrow r = \frac{{a + b - c}}
{2}}
$

Je hebt dan nu twee vergelijkingen met 2 onbekenden. Oplossen en je bent er...

$
\eqalign{\cases{
\frac{{a + b - 403}}
{2} = 74 \cr
a^2 + b^2 = 403^2
}}
$

$
\cases{
a + b = 551
\cr
a^2 + b^2 = 162.409
}
$

Zou 't dan lukken?

WvR
26-1-2009