WisFaq!

Parameterkromme

Hoe moet je een functievoorschrift voor een parameterkromme opstellen?
Ik moet namelijk een voorschrift maken van een al getekende grafiek van een kromme die als volgt is gemaakt:

y(t) = acosct+d
x(t) = dsin(et+f)

...er wordt erbij vermeld dat sin en cos veranderd mogen worden.

Als u me kunt vertellen hoe ik dit moet aanpakken (naar aanleiding van een voorbeeld), kan ik hopelijk mijn opgave maken

Alvast heel erg bedankt.

AYdin
25-1-2009

Antwoord

In het algemeen zijn er meerdere oplossingen te verzinnen. Dat betekent dat je er niet op moet rekenen dat je zomaar die a,b t/m f kunt oplossen. Je had de onderstaande grafiek opgestuurd:



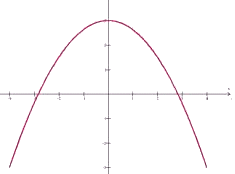
Deze grafiek wil je maken met de formules:

y(t)=a·cos ct+d
x(t)=d·sin(et+f)

Een term als +d zorgt ervoor dat de grafiek in de y richting wat opgetild wordt zodat maximum en minimum niet meer evenver van de x-as afliggen. Maar in dit geval is de d zeker 0.

Wanneer je met t=0 in de top wil beginnen is het handig om de sin bij de x te zetten en de cosinus bij de y. Dat staat er al zo dus laten we dat maar even.

y(t)=a·cos ct
x(t)=d·sin(et+f)

Die d kun je vinden door naar de uiterste waarden van de de x te kijken. (-4 en 4) en a door naar de uiterste waarden van y te kijken (-3 en 3). Dan zou je als mogelijkheden krijgen:

y(t)=3·cos ct
x(t)=4·sin(et+f)

Omdat alleen de verhouding tussen c en e de vorm bepaalt (c=1 en e=2) geeft hetzelfde resulaat als (c=37 en e=74) mag je wel c=1 kiezen.

y(t)=3·cos t
x(t)=4·sin(et+f)

Bij t=0 moet gelden dat y=4 maar dan moet ook x=0 zijn dus 4·sin(0+f)=0. Kies daarom f=0.

y(t)=3·cos t
x(t)=4·sin(et)

Nu moet bij y=-3 gelden dat x=4. y=-3 levert levert cos t=-1 zodat t=p Op dat moment moet 4 sin(et)=4 zijn dus sin(e·p)=1 dus e=0,5

y(t)=3·cos t
x(t)=4·sin(0,5t)

Dat zou het moeten doen en ook:

y(t)=3·cos (2t)
x(t)=4·sin(t)

Met vriendelijke groet
JaDeX

jadex
29-1-2009