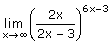
Deze limiet zou als oplossing e9 moeten hebben.
Ik kom er echter niet op uit
 x
xKan iemand me helpen, alsjeblieft?
Bedankt!
Brent
6-10-2008
Gegeven:
Deze limiet zou als oplossing e9 moeten hebben.
Ik kom er echter niet op uitx
Kan iemand me helpen, alsjeblieft?
Bedankt!Brent
6-10-2008
Schrijf eerst als een e-macht met behulp van de identiteit ab = e^(b ln(a)). De "b ln(a)" zal inderdaad een limiet zijn die je met de l'Hopital kan oplossen. Tip: als je in die uitdrukking de logaritme naar de noemer brengt ( met behulp van c = 1 / (1/c) ), dan krijg je een ¥/¥ situatie. Pobeer het eens.
Een andere leuke manier is de opgave herwerken naar de definitie van het getal e = lim (1+1/t)t. Stel dus 1+1/t = 2x/(2x-3), zodat x=(3t+3)/2 en je de limiet kan herschrijven als lim (1+1/t)^(9t+6) = [lim (1+1/t)t]9 . [lim (1+1/t)6] = e9.
cl
6-10-2008
#56669 - Limieten - 3de graad ASO