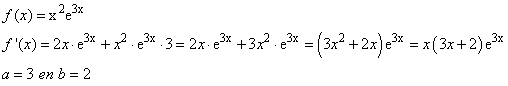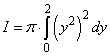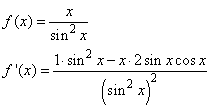WisFaq!

Re: Algebraïsch oplossen

Hoi, Bedankt!
om nog op som 4 terug te komen:
f’(x) = 2x·e^3x + x²·e^3x
(2x+x²)·e^3x
x(2+x)·e^3x

zo bereken ik toch de afgeleide goed, met de productregel? Maar ik snap niet helemaal waarom er nog een X voor staat, want er zou X(aX+b)e^3x uit moeten komen, maar dan heb je geen x na de a? (2)

dan som 3:
I(L)= integraal van a tot b p x² dy
I(L)= integraal van 0 tot 4 p x² dy
y = Öx , dus x² = y²
I(L)= integraal van 0 tot 4 p y⁴ dy
en verder kom ik niet/ snap ik het niet?

som 1. Wat is nou precies de functie van de D/DX tekens ?
afgeleide:
1/(2·sin(x)·cos(x))
Is dit zo voldoende? Of moet er nog meer mee gebeuren, ivm die d/dx?

Groeten.

gerard
2-4-2008

Antwoord

4.
Je vergeet 4. Kettingregel denk ik...



3.
Bij het wentelen om de y-as gaat het om de functie x=y² waarbij y 'loopt' van 0 tot 2. De inhoud van dat omwentelingslichaam is dan gelijk aan:



1.
Met y=f(x) dan is dy/dx een andere notatie voor de afgeleide f'(x). De afgeleide van f(x)=x/sin²(x) doe je met de 5. Quotiëntregel.



...en dan verder uitwerken.

Ik zou er maar 's wat boeken bij pakken en wat hoofdstukken gaan maken.

WvR
2-4-2008