WisFaq!

Waarom volgt mijn boek hier niet de regels die ik ken?

Dit kleine stapje snapte ik niet helemaal
Als $\sin(2t)=0$ dan is $2t=k·\pi$
Want ik heb geleerd: sinA=sinB $\to$ A=b+k·2$\pi$
Waarom antwoord mijn boek dan met k$\pi$?

emma
8-3-2008

Antwoord

Hallo Emma,
Deze opgave is ook op te lossen met de regel:

• Als sin(A)=sin(B) dan is $\angle$A=$\angle$B+k·2$\pi$ of $\angle$A=$\pi$-$\angle$B+k.2$\pi$

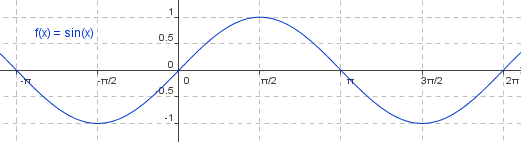
In dit geval is $\angle$B=0 dus $\angle$A=0+k·2$\pi$=k·2$\pi$ of $\angle$A=$\pi$-0+k·2$\pi$=$\pi$+k.2$\pi$
Dit is hetzelfde als $\angle$A=k·$\pi$ (zie grafiek)

wl
8-3-2008