WisFaq!

Suikerzakje

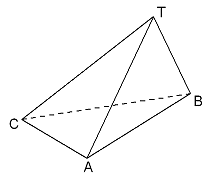
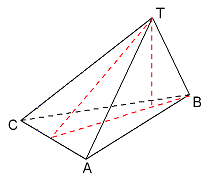
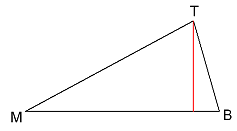
Op de foto hiernaast zie je een suikerzakje. De nuttige inhoud heeft de vorm van een driezijdige piramide.

Voor een verpakking is eerst van een rechthoekig stukje papier van 70 bij 74 mm een cilindermantel met hoogte 70 mm gemaakt. Hierbij is 4 mm voor een plakrandje gebruikt. Daarna zijn de boven- en onderkant dichtgevouwen. Ook hier is een breedte van 4 mm gebruikt voor het dichtplakken.

Het quotiënt van de nuttige inhoud en de oppervlakte van het gebruikte materiaal is een maat voor de efficiënte E van de verpakking.

1. Bereken voor dit suikerzakje de waarde van E.
2. Bereken de waarde van E voor zo'n verpakking waarbij alle afmetingen twee keer zo groot zijn.
3. Bereken de waarde van E als de afmetingen van het gebruikte papier twee keer zo groot zijn, maar waarbij de plakrandjes 4 mm blijven.

Mvg

micky beerens
25-2-2008

Antwoord

Eerst maar 's een tekening:



Als ik dat zo zie dan vermoed ik dat dit lichaam bestaat uit 4 gelijke gelijkbenige driehoeken. De 'totale oppervlakte' moet niet moeilijk zijn. De vraag is nu: wat is de inhoud?

De inhoud is gelijk aan éénderde van de oppervlakte van het grondvlak vermenigvuldigd met de hoogte of wel:

Inhoud=¹/₃·G·h

G zou bekend moeten zijn en h zou je dan moeten kunnen berekenen. Ik heb nog maar 's wat hulplijntjes getekend:



Daarmee zou het moeten kunnen. Je moet maar bedenken dat die driehoek met de hoogtelijn ook weer gelijkbenig is...



Ik heb 't zelf nog niet geprobeerd, maar wij hoeven natuurlijk niet alles te doen. Misschien kan je er nu zelf verder mee. Ik zie 't wel zitten, ergens...

WvR
26-2-2008