WisFaq!

Pincode raden

Dit is een som uit mijn boek, ik begrijp hem niet en de antwoorden in het antwoordenboek kloppen niet, zou u deze som heel uitgebreid en stap voor stap aan mij uit willen leggen?

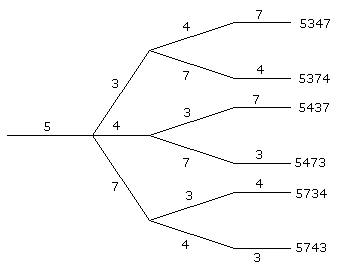
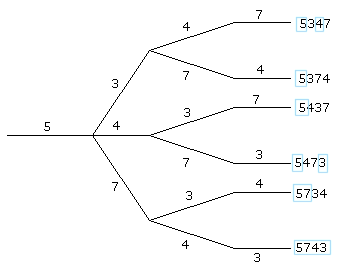
Daar sta je dan 's avonds laat voor de geldautomaat! was het 5734 of 5347....? Het enige wat je nog zeker weet is dat je pincode bestaat uit de vier cijfers 3,4,5 en 7 en dat de code begint met 5. Dat wordt proberen........en het pasje wordt geblokkeerd na drie foute pogingen.

1. Hoeveel verschillende pincodes zijn er dan mogelijk? (dit lijkt me 3!=6. want het eerste cijfer weet je al zeker en de overige 3 zijn op 3! manieren te rangschikken)

2. Stochast X is het aantal cijfers dat bij een poging op de juiste positie staat. Hoe ziet de kansverdeling van X eruit? (wilt u hierbij alstublieft heel duidelijk uitleggen hoe u aan elke kans gekomen bent, en dus niet de laatste kans met 1 - de al gevonden kansen berekenen?)

3. Bereken de kans dat het met willekeurig proberen lukt om geld uit de machine te krijgen.

4. Bepaal E(X) en Var(X)

Alvast heel erg bedankt voor het beantwoorden van mijn vraag!!!

anne zwart
16-11-2002

Antwoord

Ik ga er vanuit dat je 'zeker' weet dat het eerste cijfer een vijf is en dat willekeurig proberen alleen slaat op de laatste drie cijfers.

1. 3!=6 lijkt me ok
   
   
2. Teken een kansboom!
   
   
   
   Laten we eens aannemen dat de laatste de goede pincode is. Dan kun je bij de andere mogelijkheden kijken hoeveel cijfers er op de goede positie staan:
   
   
   
   Je ziet:
   P(X=0)=0
   P(X=1)=2/6
   P(X=2)=3/6
   P(X=3)=0
   P(X=4)=1/6
   
   
3. De kans dat het na 1 keer lukt is 1/6
   De kans dat het na 2 keer lukt is 5/6·1/5
   (het is dan wel laat, maar ik ga natuurlijk niet nog een keer dezelfde pincode proberen!)
   De kans dat het na 3 keer lukt is 5/6·4/5·1/4
   Als het dan nog niet gelukt kan je het wel schudden, dus de kans is:
   1/6+5/6·1/5+5/6·4/5·1/4=1/2
   
   
4. E(x)=1·2/6+2·3/6+4·1/6=2
   Var(x)=E(x²)-(E(x))²
   Var(x)=1·2/6+4·3/6+16·1/6-2²
   Var(x)=5-4=1

WvR
17-11-2002