WisFaq!

Twee exponentiele functies snijden

Goeiedag,
stel, ik heb twee sets van ieder vier sets x en y coordinaten.
Als ik deze twee sets van vier punten in een grafiek teken dan lijken de grafieken op exponentiele functies(dus twee stuks).
Als ik van alle y waarden het natuurlijk logaritme neem en die vervolgens uitzet in een grafiek, dan lijken beiden een min of meer rechte lijn te vormen. Vraag: is hiermee bewezen dat de oorspronklijke functie op een exponentiele functie lijkt?

Vraag 2: Als ik de twee rechte lijnen benader waaruit y=ax+b komt voor de eerste en y=cx+d voor de tweede, en beide vervolgens aan elkaar gelijkstel, krijg ik dan de x-coordinaat waarop de beide oorspronkelijke(exponentiele) functies elkaar snijden?

Joost
14-11-2002

Antwoord

Vraag 1
Op Logaritmische schalen kun je lezen dat een exponentiële functie op enkellogaritmisch papier een rechte lijn geeft. Dus de stelling 'als een grafiek op enkellogaritmisch papier een rechte lijn is, dan heb je te maken met een exponentiëel verband' wel gerechtvaardigd.

Vraag 2
Vast wel. Laten we maar eens naar een voorbeeld kijken. Je ziet hieronder de grafieken van twee exponentiële functies:



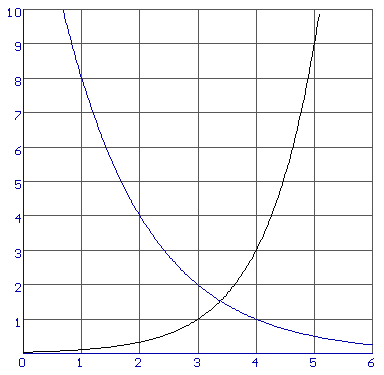
Als ik dezelfde grafieken op enkellogaritmisch papier teken dan krijg ik deze figuur:



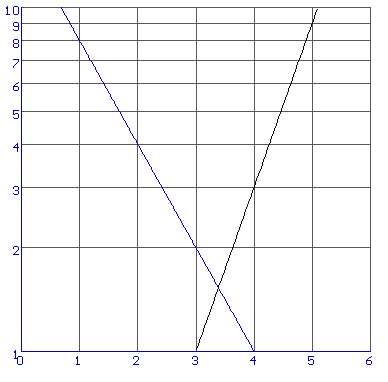
Zoals je ziet verandert er aan de coördinaten van het snijpunt niets. Wat verandert is de plaats (op het papier) van de punten, maar de coördinaten niet...

WvR
17-11-2002