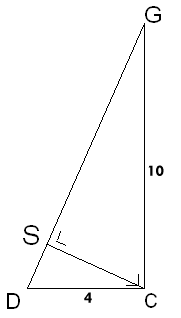
In \DeltaDCG geldt:
\DeltaDCG~CSG (gelijkvormigheid)
DG=√116
Met een verhoudingstabel kan je dan de lengte van CS bepalen.
Zie Oefenopgaven gelijkvormigheid voor voorbeelden met antwoorden (met name opgave 1).
WvR
20-10-2007
Graag zou ik hulp krijgen bij de volgende opdracht:
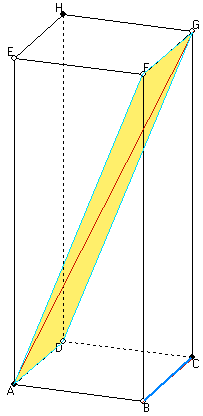
ABCD.EFGH is een balk met AB=BC=4 en CG=10.
Construeer en bereken de lengte van het kortste verbindingslijnstuk van AG en BC.
Mijn antwoord:
\DeltaCDG^BC
DG is projectie van AG op CDG
C is projectie van BC op CDG
CK^DG is kortste lijnstuk
P = AG \cap lijn door K//AD
Q = BC \cap lijn door P//CK
Om deze lengte te berekenen heb ik \DeltaDCG getekend, maar hoe dan verder?
Bedankt alvast!Tjen
20-10-2007
Een goed plan! Want BC is evenwijdig aan ADGF. En als je dan in de richting van AD kijkt...
In \DeltaDCG geldt:
\DeltaDCG~CSG (gelijkvormigheid)
DG=√116
Met een verhoudingstabel kan je dan de lengte van CS bepalen.
Zie Oefenopgaven gelijkvormigheid voor voorbeelden met antwoorden (met name opgave 1).
WvR
20-10-2007
#52596 - Ruimtemeetkunde - Student hbo