WisFaq!

Hoeken berekenen

Gegeven is vierkant ABCD . Binnen dit vierkant ligt een punt E zó dat $\angle$ cde = $\angle$dce = 15°
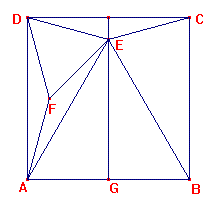
Bereken exact $\angle$EAD
In het antwoord mogen geen uitdrukkingen staan als sinus, cosinus, tangens etc.



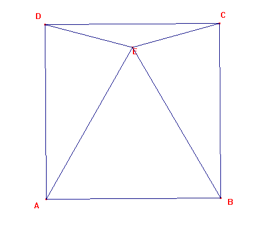
Deze som moet ik voor het vak wis D oplossen. maar ik snap hem niet. Ik heb verschillende vergelijken gemaakt, maar ze komen steeds uit op 180=180 of x=x of x=0 en dit klopt niet ook ben ik erachter gekomen dat dit figuur uit 8 driehoekjes bestaat. ik ben er achter gekomen dat $\angle$ADE 75 ° is. zo ook hoek ECD.
hoek DEC = 150 °
hoek DAE = x °
dan = hoek AEB 2x°
hoek EAB en hoek EBA zijn 90 - x °
hoek DEA en hoek BEC zijn 105 - x °

Ik hoop dat u mij kan helpen deze som op te lossen, ik weet niet zeker op dit de goede categorie is maar ik kon de categorie hoeken niet vinden.
BVD

Marieke Hoogvliet
8-10-2007

Antwoord

Dag Marieke,
Zoals wel vaker zijn er meerdere wegen naar Rome.

Je kan het goniometrisch oplossen:
Stel de zijden van het vierkant zijn 2.
Dan is EG=2-tan(15^o).
Met de verdubbelingsformules vindt je:
tan(2x)=2tan(x)/(1-tan²(x))
tan(2x)=tan(30^o)=¹/₂√3.
Links en rechts vermenigvuldigen met (1-tan²(x)) geeft:
¹/₂√3(1-tan²(x))=2tan(x)
Dit geeft een tweedegraads vergelijking in tan(15^o) die je met de abc-formule kan oplossen.
En dan invullen in de vergelijking voor EG.

Het kan ook met: tan(2x)=sin(2x)/cos(2x)
cos(2x)=1-2sin²(x), dus sin(x)=√¹/₂√(1-cos(2x))
cos(2x)=2cos²(x)-1, dus cos(x)=√¹/₂√(1+cos(2x)).
Vul maar in en vereenvoudig.(cos(30^o)=1/√3)
Als je het goed doet vindt je: GE=√3. Maar dan is hoek GAE=60^o.



Meetkundig kan het nog makkelijker, maar je moet wel op het idee komen:
Bedenk dat hoek ADE=75^o. En 75=60+15
Je kan dus $\Delta$AFD tekenen die congruent is met $\Delta$DEC.
Trek ook EF.
Waarom is $\Delta$DEF gelijkzijdig?
Gevolg: $\Delta$AEF is gelijkbenig en de tophoek AFE=?
En hoe groot is $\angle$FAE?

ldr
8-10-2007