WisFaq!

Bewijs snijpunt hoogtelijnen van een driehoek

Hoe bewijs ik dat de drie hoogtelijnen van een driehoek elkaar in 1 punt snijden?

Dennis
3-11-2002

Antwoord

We gaan ervan uit dat de hoogtelijnen uit B en C elkaar snijden in het punt S. Zie onderstaand plaatje.



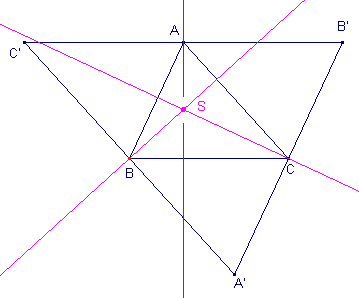
We willen bewijzen dat de hoogtelijn uit A door het punt S gaat.
We tekenen een tweede driehoek A'B'C' zo, dat

• A'B' // AB en A'B' gaat door C
• B'C' // BC en B'C' gaat door A
• C'A' // CA en C'A' gaat door B

Beantwoord nu zelf de volgende vragen:

• Waarom staat de hoogtelijn uit A loodrecht op B'C'?
• Waarom staat de hoogtelijn uit B loodrecht op A'C'?
• Waarom staat de hoogtelijn uit C loodrecht op A'B'?

Nu kijken we naar de volgende vierhoeken: BCAC' en BA'CA.

• Waarom zijn dat parallellogrammen?
• Die beide parallellogrammen hebben een zijde gemeenschappelijk (AC).
• Waarom zijn dan BA' en BC' aan elkaar gelijk?

En dan de belangrijkste conclusie:

• Waarom is nu de hoogtelijn uit B ook de middelloodlijn van A'C'?
• Waarom is de hoogtelijn uit C de middelloodlijn van A'B'?

Ook de hoogtelijn uit A is middelloodlijn.

• Waarom? En van welke zijde van driehoek A'B'C'?

Tja, meetkunde is een deductieve wetenschap. Je moet dus (bijna altijd) eerder opgedane kennis omtrent de figuren gebruiken. Naar ik hoop ken je de volgende stelling:

• De middelloodlijnen van een driehoek (bekijk A'B'C) snijden elkaar in één punt.
• Welk punt is dat dan in dit geval?

Het antwoord op de laatste vraag heb je nu wel:

• Waarom gaat de hoogtelijn uit A ook door het punt S?

dk
3-11-2002