WisFaq!

Logaritmische vergelijking

Hoe los ik de volgende vergelijking op?
10log(N)- 0,00512(N)= 25,79748
Ik kom er met geen mogelijkheid uit.....
Alvast bedankt voor de moeite!
Groeten van Femke

Femke Hoogervorst
31-10-2002

Antwoord

Hoi Femke,

Je vergelijking kan je niet algebraïsch oplossen. Je kan wel de grafiek tekenen van y=(10.log(x)-25.79748)/0.00512 en y=x en het snijpunt zoeken.
Dit geeft:




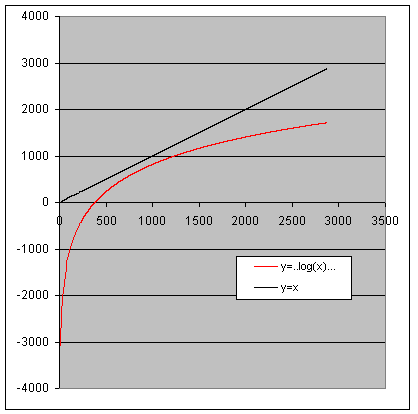
Zoals je ziet... geen oplossing. Je kan dit ook bewijzen door het tekenverloop en een minimum te bepalen, maar dat is je vraag niet.

Daarom dacht ik dat je misschien ln(x) ipv log(x) bedoelde (grondtal e ipv 10).

y=(10.ln(x)-25.79748)/0.00512 en y=x:



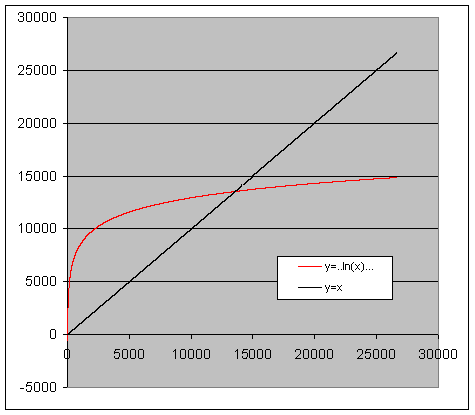
We zien dat er nu 2 oplossingen zijn, eentje 'dicht bij 1' en eentje rond 14000.

Je kan iteratief naar een oplossing zoeken.
Daarvoor bekijken we de volgende rijen die convergeren naar oplossingen:
x₀=15000
x_k+1=(10.ln(x_k)-25.79748)/0.00512
x₂₀=13,542.68296

x₀=10
x_k+1=exp((25.79748+0.00512x_k)/10)
x₂₀=13.28385

In Excel kan je het nog makkelijker met 'Goal Seek' vinden.
Je moet dan wel de goeie beginwaarden geven.

Eigenlijk zouden we nu moeten onderzoeken hoe nauwkeurig dit is, maar ik denk dat je hiermee al voort kan. Er bestaan andere rijen die eventueel sneller convergeren, maar dit is al een heel onderzoek op zich (waarvoor ik een paar cursussen van x jaar geleden bij de hand zou moeten nemen).

Groetjes,
Johan

andros
31-10-2002