WisFaq!

Re: Oplossen van IVP

Bedankt.

ik heb nog 2 kleine vraagjes over differentiaal vergelijkingen, kan ik deze aan u stellen?

opgave:
y'=2+e^y
uiteindelijk: òe^-y=ò2 dt.
hieruit krijg ik -e^-y/ln[e]=2t + C, hoe kom ik tot de uitkomst y=-ln(Ce^(-2t) -1/2)(boek), krijg geen goede uitkomst uit mathematica.
tweede vraag:
y'=1-y^2
krijg hieruit :
-1/2Ln[-1+y]+1/2Ln[1+y]=x + C
hier kom ik niet meer verder...
mathematica geeft als uitkomst: y=(e^2x + e^2C)/(e^2x - e^2C)

bij voorbaat heel veel dank.

gr.
moos

moos
5-5-2007

Antwoord

dag Moos,

eerste opgave: hier heb je de methode van het scheiden van variabelen niet goed uitgevoerd.
Het moet als volgt:

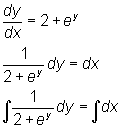
De integraal links kun je uitwerken door de teller van de breuk te schrijven als ¹/₂(2 + e^y - e^y) en daarmee de breuk te splitsen. Lukt dat?
Er komt overigens wel een ander antwoord uit dan het boek geeft...
tweede opgave: Van de twee logaritmen kun je één logaritme maken.
Werk dan de factor ¹/₂ naar de andere kant.
neem van beide kanten de e-macht, zodat de logaritme wegvalt.
Je houdt dan links een breuk over met y in de teller en in de noemer.
Splits deze breuk zodat er komt te staan: a + ^b/_(y-1)
Werk hieruit de y vrij, en je krijgt het gegeven antwoord.

Anneke
6-5-2007