Algoritme van Euclides
Hieronder zie je het stroomschema dat hoort bij het Algoritme van Euclides.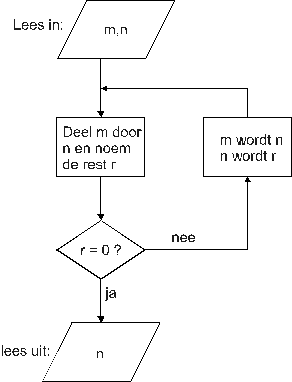
m en n zijn twee natuurlijke getallen, waarbij m > n
Voorbeeld:
Je begint met: m = 24 en n =15 dan r = 9
Na één stap krijg je: m = 15 en n = 9 dan r = 6
Na de tweede stap: m = 9 en n = 6 dan r = 3
Een stap later: m = 6 en n = 3 dan r = 0
Nu is r gelijk aan 0, het algoritme stopt. n heeft de waarde 3.
GGD met ontbinden in priemfactoren
Voorbeeld:9191 = 7 · 13 · 101
1001 = 7 · 11 · 13
Nu hebben 9191 en 1001 de factoren 7 en 13 gemeenschappelijk.
Dus GGD(9191,1001)=91 (7×13)
Zeef van Erastosthenes
Deze vraag is al eerder beantwoord: pag.75.Zeef van Ulam
Daar kunnen we niet zo veel over vinden. Misschien bedoelt je docent:"Ulam's Problem (Searching with Lies):
Someone chooses an integer between 1 and 1,000,000. You get to ask YES or NO questions to determine the number. However, the other person is allowed to lie in response to at most one of your answers. How many questions do you need to determine the chosen number? What is the best sequence of questions to ask? Of course we are also interested in the more general problem where the selected number is between 1 and n and the person is allowed to lie at most k times."
Problems.html
Wij denken dat het in nml35.html uitvoerig beschreven staat.
In Chapter 2 (s.10), "Algorithms in Number Theory" staat:
- Square-free Integers
- Sieve of Eratosthenes
- A Formula for an Irregular Sequence
- An Olympiad Problem
- Ulam's Sequence
Misschien heb je hier nog iets aan:zoekopdracht
WvR
30-10-2001